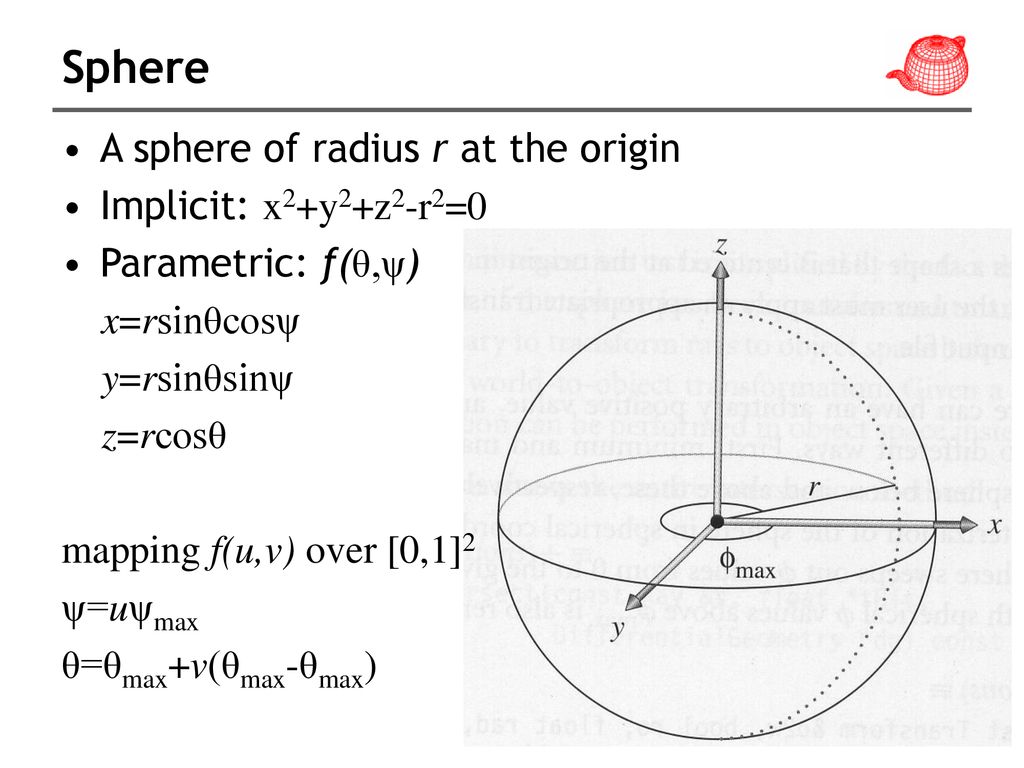
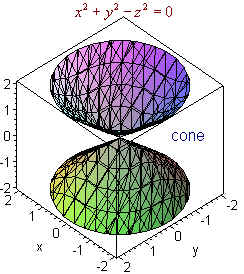
√完了しました！ x^2 y^2 z^2=r^2 graph 282099

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!(e) Below is the graph of z = x2 y2 On the graph of the surface, sketch the traces that you found in parts (a) and (c) For problems 1213, nd an equation of the trace of the surface in the indicated plane Describe the graph of the trace 12 Surface 8x 2 y z2 = 9;Two more topics We need to massive equations with the grass The first toe Russell this so we could see that this is a parable, Lord

Comparison Between The Distribution Of V Y R R 2 R 500 In A Graph Download Scientific Diagram

X^2 y^2 z^2=r^2 graph

X^2 y^2 z^2=r^2 graph-And by the symmetry of uin xand y, u yy= 2x2 22y (x2 y2)2 Clearly then u xx u yy= 0 in this case If u= arctan(y=x), then by the chain rule again u x= 1 1 (y x) 2 y x 2 = 2y x y 2) u xx= (x y2)(0) ( y)(2x) (x y22 SURFACES Definition A subset S R3 is a regular surface if, for each point p S , there is an open neighborhood V of p in R3, an open set U R2 and a map X U V S , such that (1) X is smooth, meaning that if we write X(u, v) = (x(u, v), y(u, v), z(u, v)) , then the realvalued functions x(u, v) , y(u, v) and z(u, v)

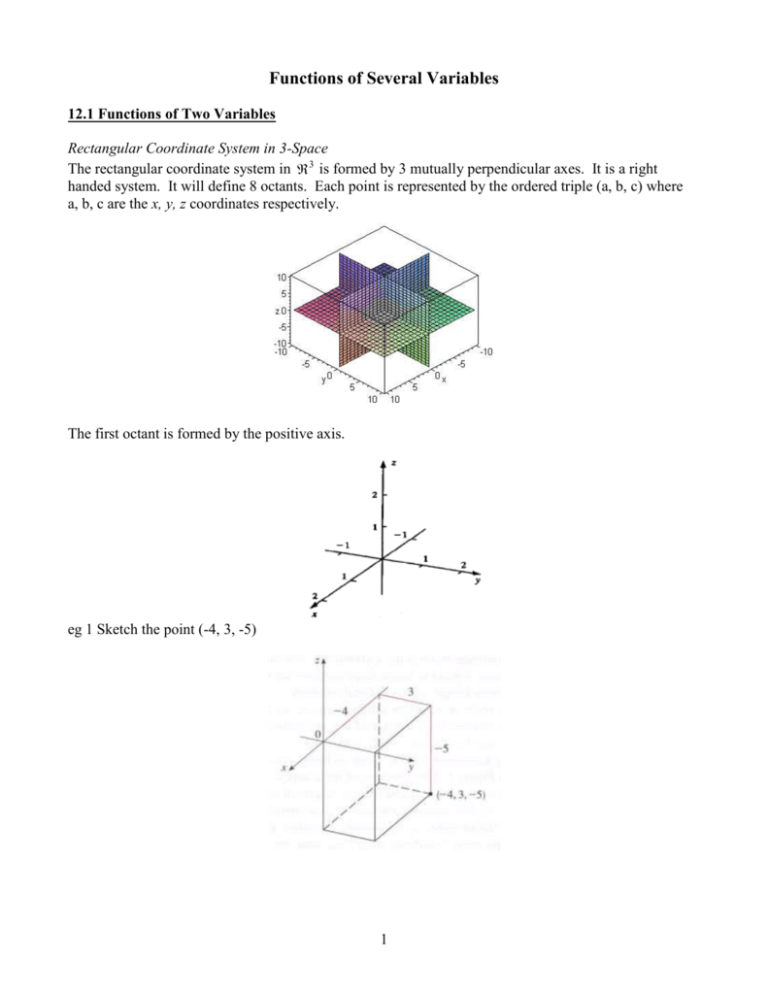
Functions Of Several Variables

Graphs (z= f(x;y)) The graph of f R2!R is f(x;y;z) 2R3 jz= f(x;y)g Example When we say \the surface z= x2 y2, we really mean \The graph of the function f(x;y) = x2 y2 That is, we mean the set f(x;y;z) 2R3 jz= x2 y2g Level Sets (F(x;y;z) = c) The level set of F R3!R at height cis f(x;y;z) 2R3 jF(x;y;z) = cgWhat I usually do is break a threedimensional graph up into three separate planes, XY, XZ, YZ, and I draw them individually and try to visualize how they fit togetherAll the surfaces have been the graph of some quadratic relation in $x,\, y,$ and $z$ like $z x^2 y^2 = 0$ in the case of a hyperbolic paraboloid or $x^2 y^2 z^2 = r^2$ for a sphere, all the crosssections of these surfaces have been conic sections like parabolas, hyperbolas etc In view of the first of these comments we make the following

1269(a)Find and identify the traces of the quadric surface x2 y2 z2 = 1 and explain why the graph looks like the graph of the hyperboloid of one sheet in Table 1 x= k)k2 y2 z2 = 1 )y2 z2 = 1 k2 The trace is a hyperbola when k6= 1 If k= 1, y2 z2 = (yz)(y z) = 0, so it is a union of two lines y= k)x2 k2 z2 = 1 )x2 z2 = 1 k2 The trace isThe graph of a 3variable equation which can be written in the form F(x,y,z) = 0 or sometimes z = f(x,y) (if you can solve for z) is a surface in 3D One technique for graphing them is to graph crosssections (intersections of the surface with wellchosen planes) and/or traces (intersections of the surface with the coordinate planes)Substitute r 2 = x 2 y 2 r 2 = x 2 y 2 into equation r 2 z 2 = 9 r 2 z 2 = 9 to express the rectangular form of the equation x 2 y 2 z 2 = 9 x 2 y 2 z 2 = 9 This equation describes a sphere centered at the origin with radius 3 3 (see the following figure)

If one of the variables x, y or z is missing from the equation of a surface, then the surface is a cylinder Note When you are dealing with surfaces, it is important to recognize that an equation like x2 y2 = 1 represents a cylinder and not a circle The trace of the cylinder x 2 y = 1 in the xyplane is the circle with equations x2 y2Plotting graphics3d Share Improve this question Follow asked Nov 29 '15 at 533 user userX(1) = 1 = y z^2 the xz plane creates a hyperbole y(1) = 1 = x^2 z^2 We know that this creates a hyperbolic paraboloid (xy plane creates a parabola up, xy creates parabola down, shaped by a hyperbole from the top saddle like figure) the only hyperbolic paraboloid is graph V

Quadratic Function Wikipedia

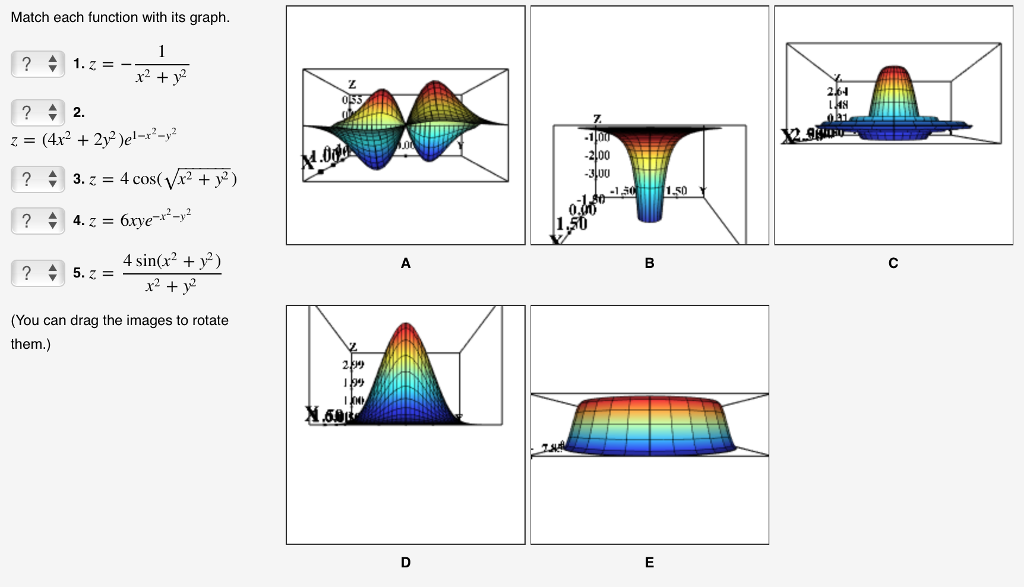
Solved Match Each Function With Its Graph I Z R2 Y2 2 Chegg Com

Conic Sections (see also Conic Sections) Point x ^2 y ^2 = 0 Circle x ^2 y ^2 = r ^2 Ellipse x ^2 / a ^2 y ^2 / b ^2 = 1 Ellipse x ^2 / b ^2 y ^2 / a ^2 = 1 Hyperbola x ^2 / a ^2 y ^2 / b ^2 = 1 Parabola 4px = y ^2 Parabola 4py = x ^2 Hyperbola y ^2 / a ^2 x ^2 / b ^2 = 1 For any of the above with a center at (j, k) instead of (0,0), replace each x term with (xj) andNow we save thisWays to Visualize functions f R !R (eg f(x) = x2) (1) SetTheoretic Picture (2) Graph of f (Thinking y= f(x)) The graph of f R !R is the subset of R2 given by Graph(f) = f(x;y) 2R2 jy= f(x)g (3) Level sets of f

14 1 Functions Of Several Variables Mathematics Libretexts

4 2 3d Graphing Graphing Calculator By Mathlab User Manual

A sphere is the graph of an equation of the form x 2 y 2 z 2 = p 2 for some real number p The radius of the sphere is p (see the figure below) Ellipsoids are the graphs of equations of the form ax 2 by 2 c z 2 = p 2 , where a , b , and c are all positiveExplanation Considering the variables x,y,z defining R3, this geometrical object is a surface such that for any x obeys y2 z2 = 16 so it is a cylindrical surface centered at the x axis having a circle with radius 4 as transversal cross section Answer linkAnswer (1 of 10) Suppose f(x,y) = x^2 y^2 Let's look at the partial derivatives of this function \displaystyle\frac{\partial f}{\partial x}= 2x \displaystyle\frac{\partial f}{\partial y}= 2y So apparently, at each (x,y) coordinate pair (black dots below), the gradient of f(x,y) is pointin

2 D And 3 D Plots Matlab Simulink

Setting Up An Integral Over A Solid With Order Of Integration Dr D8 Dz

Steps to graph x^2 y^2 = 4The graph of the function EXERCISE 7 f (x, y) = x 2 y 2 is the cone z = x 2 y 2 Find the equation of the tangent plane at the point (3, − 4, 5) Show that the tangent plane at any point on the cone in Exercise 1 passes through the EXERCISE 8 originHow to plot 3 dimensional graph for x^2 y^2 = 1?

2

Solved Match The Equations Of The Surface With The Graphs Chegg Com

Given equations to where it's placed TV minus their visible to fight forex kwehr bodies What about when I was a good one?For all x;y 2C, x 6= y, and 2(0;1), then we say that f(x) is strictly concave Intuitively, the graph of a convex function lies on or below any chord between two points on the graph2B2 a) Find the equation of the tangent plane to the cone z = x2 y2 at the point P 0 (x 0 ,y 0 ,z 0 ) on the cone b) Write parametric equations for the ray from the origin passing through P 0 , and

How To Plot 3d Graph For X 2 Y 2 1 Mathematica Stack Exchange

1

Plane z = 1 The trace in the z = 1 plane is the ellipse x2 y2 8 = 1X 2 y 2 = r 2 For a sphere you need to use Pythagoras' theorem twice In the diagram below O is the origin and P(x,y,z) is a point in 3space P is on the sphere with center O and radius r if and only if the distance from O to P is r The triangle OAB is a right triangle and hence x 2 y 2 = s 2The cone z = sqrt (x^2 y^2) can be drawn as follows In cylindrical coordinates, the equation of the top half of the cone becomes z = r We draw this from r = 0 to 1, since we will later look at this cone with a sphere of radius 1 >

Level Set Examples Math Insight

Functions Of Several Variables

Surfaces and Contour Plots Part 4 Graphs of Functions of Two Variables The graph of a function z = f(x,y) is also the graph of an equation in three variables and is therefore a surfaceSince each pair (x,y) in the domain determines a unique value of z, the graph of a function must satisfy the vertical line test already familiar from singlevariable calculusThe square root keeps us from going above that point z=4 if we manipulate the equation and isolate x 2 y 2 we get x 2 y 2 = 16 z 2 (remember that since we have a square root in our original function, we have to consider it's domain in our graph, meaning z <=4) This is the equation of a cone so we now know what we are looking atExport less wise Quarter Birdman line minus that squares with one export less by sportive Urban nine with export And why is it good?

Find The Volume Of The Given Solid The Solid Bounded By The Cylinders X 2 Y 2 16r 2 Y 2 Z 2 16r 2 Study Com

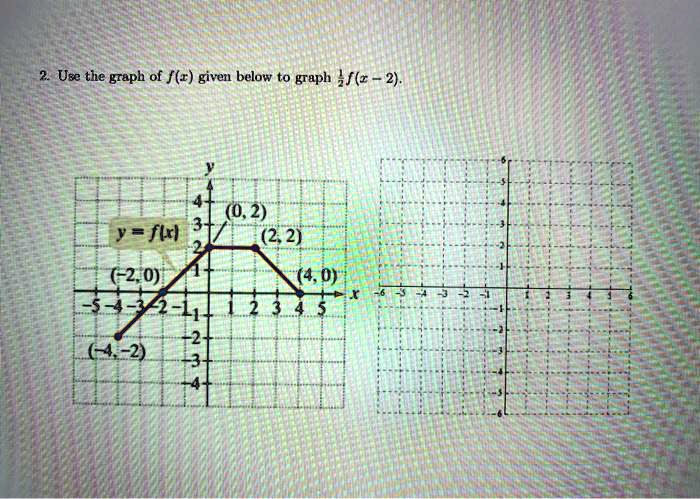
2obto3f2j43oxm

Free functions and graphing calculator analyze and graph line equations and functions stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyI am already using it and I only can plot in 2 dimensional graph Can someone help me with this problem?Z=x^2y^2 WolframAlpha Volume of a cylinder?

X 2 Y 2 Z 2 0 Graph Dawonaldson

How To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange

Example 2 f(x,y,z) = x 2 z 2, the level Surfaces are the concentric cylinders x 2 z 2 = c with the main axis along the y axis With some adjustments of constants these level surfaces could represent the electric field of a line of charge along the y axis Here we have f = 2,4,8,12, and 16#x^2 6x y^2 4y = 12 Then take 1/2 of the 'b' term for both quadratic expressions, square those values and add them to both sides #x^2 6x 9 y^2 4y 4 = 12 9 4 (x 3)^2 (y 2)^2 = 25 Circle centered at (3,2) with radius = 5If u= log(x2 y2), then by the chain rule u x= 2x x 2 y) u xx= (x2 y2)(2) (2x)(2x) (x 2 y) = 2y2 2x2 (x y2)2;

If X X 1 X 2 Represents

Find The Volume Of Region Bounded By The Paraboloid Z 25 X 2 Y 2 And The Xy Plane Study Com

The parametric equations are x= t2, y= t4, z= t6 These are positive for t 6= 0 and 0 when t = 0 So the curve lies entirely in the first quadrant The projection of the graph onto the xyplane is y = x2, y>0 , a half parabola On the xzplane z = x3, z >0, a half cubic, and the yzplane, y3 = z2, as indicated in the graph (g) r(t) = t2itj2kGiven a matrix (x, y, z) where z is the heights it will plot both the points and also a surface Limitations are that there can only be one z for each (x,y) pair So planes which loop back over themselves will cause problems The plot_points = T will plot the individual points from which the surface is made this is useful to check that theA quick video about graphing 3d for those who never done it before Pause the video and try it

Comparison Between The Distribution Of V Y R R 2 R 500 In A Graph Download Scientific Diagram

How To Construct The Graph Of X 2 Y 2 9 Quora

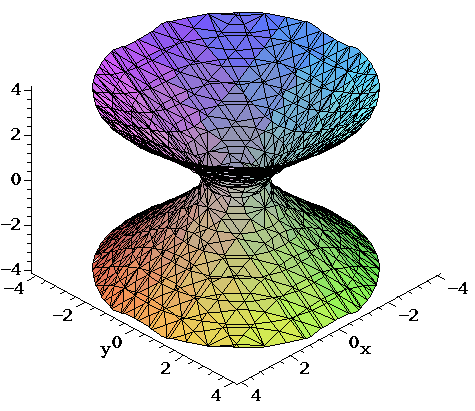
Transcribed image text An equation for the tangent plane to the graph of z = rºy2 y when (r, y) = (1, 1) is O 3x y z = 2 O 3x y 2 2 O 3x Y 2 2 O 3x y 2 2 O None of these Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator COMPANY1;z 1) and Q(x 2;y 2;z 2) is jPQj= p (x 2 x 1)2 (y 2 y 1)2 (z 2 z 1)2 EXAMPLE 5 Show that the equation x2 y2 z2 2x 4y8z17 = 0 represents a sphere, and nd its center and radius In general, completing the squares in x2 y2 z2 Gx Hy Iz J= 0 produces an equation of the form (x a)2 (y b)2 (z c)2 = k If k>0 then the graph of3 Answers3 Write it as x 2 z 2 = y 2 Note that y is the hypotenuse of a triangle with length x and height z So, this forms a circular cone opening as you increase in y or decrease in y This figure is the (double) cone of equation x 2 = y 2 − z 2 The gray plane is the plane ( x, y) You can see that it is a cone noting that for any y

2 3 Tangent Plane To A Surface Mathematics Libretexts

Surfaces Part 2

Graph x^2y^2=r^2 Move all terms containing variables to the left side of the equation Tap for more steps Subtract from both sides of the equation Move Reorder and This is the form of a hyperbola Use this form to determine the values used to find vertices and asymptotes ofPiece of cake Unlock StepbyStep Natural Language Math InputAssignment 7 Solutions Math 9 { Fall 08 1 (Sec 154, exercise 8) Use polar coordinates to evaluate the double integral ZZ R (x y)dA;

70以上 Y2x2 Z2 ニスヌーピー 壁紙

2

Graph y^2z^2=9 y2 z2 = 9 y 2 z 2 = 9 Reorder terms x2 y2 = 9 x 2 y 2 = 9 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard formWhere Ris the region that lies to the left of the yaxis between the circles x2 y2 = 1 and x2 y2 = 4 Solution This region Rcan be described in polar coordinates as the set of all pointsQuestion Sketch the graph of z = x^2 y^2 in R^3 Name the surface (a) Paraboloid (b) Ellipsoid (c) Circle (d) Hyperboloid Find the domain of the function f (x, y) = ln (x y^2) (a) All points on or to the right of x = y^2 (b) All points on or to the right of x = 0 (c) All points on or to the left of x = 0 (d) All points on or to the left

Lab Html

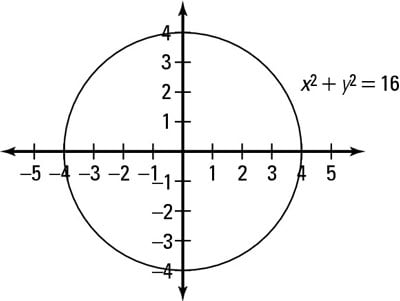
2 Ways To Graph A Circle Dummies

In the twodimensional coordinate plane, the equation x 2 y 2 = 9 x 2 y 2 = 9 describes a circle centered at the origin with radius 3 3 In threedimensional space, this same equation represents a surface Imagine copies of a circle stacked on top of each other centered on the zaxis (Figure 275), forming a hollow tubeCircle on a Graph Let us put a circle of radius 5 on a graph Now let's work out exactly where all the points are We make a rightangled triangle And then use Pythagoras x 2 y 2 = 5 2 There are an infinite number of those points, here are some examples3D plot x^2y^2z^2=4 WolframAlpha Natural Language Math Input Extended Keyboard Examples

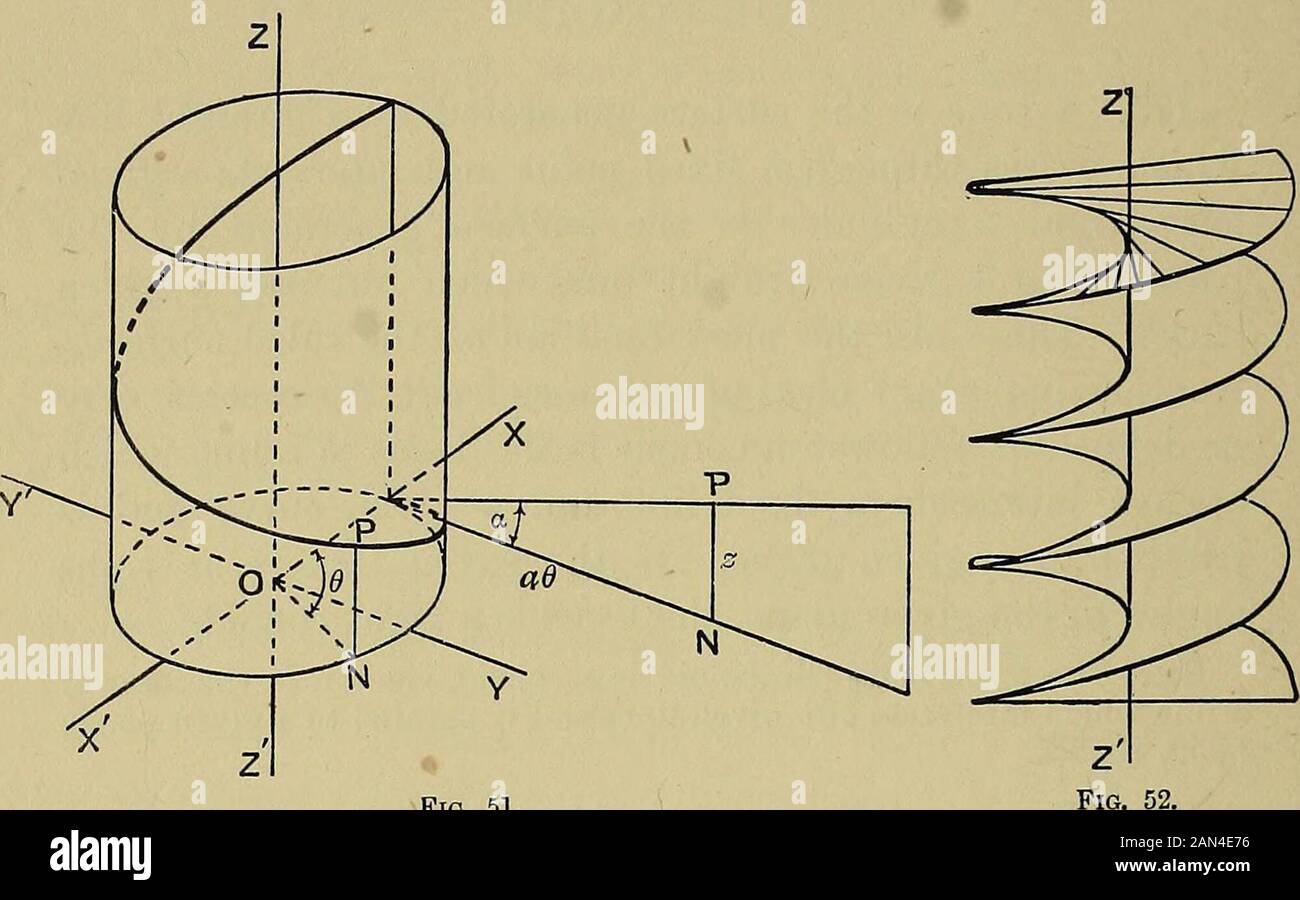
An Elementary Treatise On Coordinate Geometry Of Three Dimensions Il We Obtain The Equation To The Conoid Viz Z F Y X Ex 1 Find The Equation To The Right Conoid Generated By Lineswhich

X 2 Y 2 Z 2 0 Graph Dawonaldson

2 We can describe a point, P, in three different ways Cartesian Cylindrical Spherical Cylindrical Coordinates x = r cosθ r = √x2 y2 y = r sinθ tan θ = y/x z = z z = z Spherical Coordinates x = ρsinφcosθ ρ = √x2 y2 z2 y = ρsinφsinθ tan θ = y/x z = ρcosφ cosφ = √x2 y2 z2 zSurface area of x^2 y^2 z^2 = r^2 So I tried to integrate the function for a sphere to find the surface area and rotate it to find the volume, not hypervolume, of a hypersphere I tried a few times and kept getting (128/3)×𝜋×r 3 ×i×r 3 I used the equation for the surface area a 3D graph, S=∬ (1 (dz/dx) 2 (dz/dy) 2 dX dy I do\{x^2} {z^2} = {r^2}\ With this in hand we can arrive at the limits of the variables that we'll need for this integral \\begin{array}{c}2{x^2} 2{z^2} \le y \le 8\\ 0 \le r \le 2\\ 0 \le \theta \le 2\pi \end{array}\ The integral is then,

2

Homework 3 Model Solution Han

Answer (1 of 3) It's the equation of sphere The general equation of sphere looks like (xx_0)^2(yy_0)^2(zz_0)^2=a^2 Where (x_0,y_0,z_0) is the centre of the circle and a is the radious of the circle It's graph looks like Credits This 3D Graph is created @ code graphing calculator

1 Sketch The Surface Z X 2 Y 2 2 Sketch The Surface Z 2y 2 4x 2 Study Com

1

10 1 Circles 1 X Y R Higher Maths Lessons Mrthomasmaths X2 Y2 R2 X 2 Y 2 R 2 Youtube

Surfaces

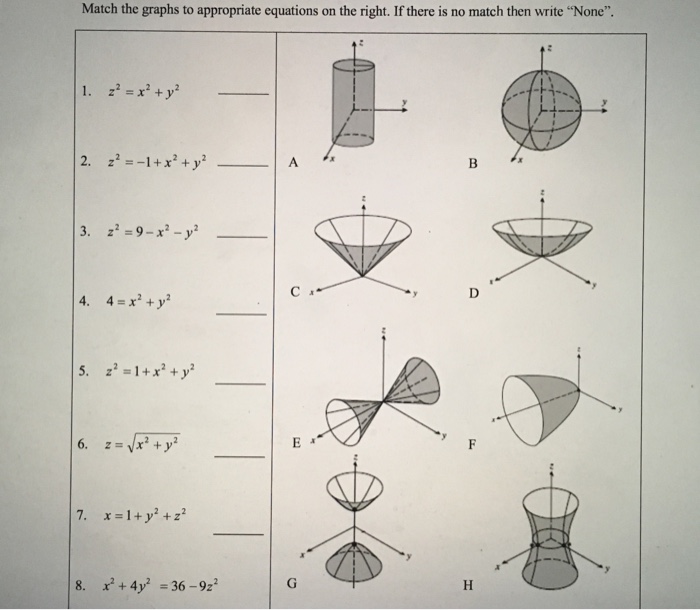
Solved Match The Graphs To Appropriate Equations On The Chegg Com

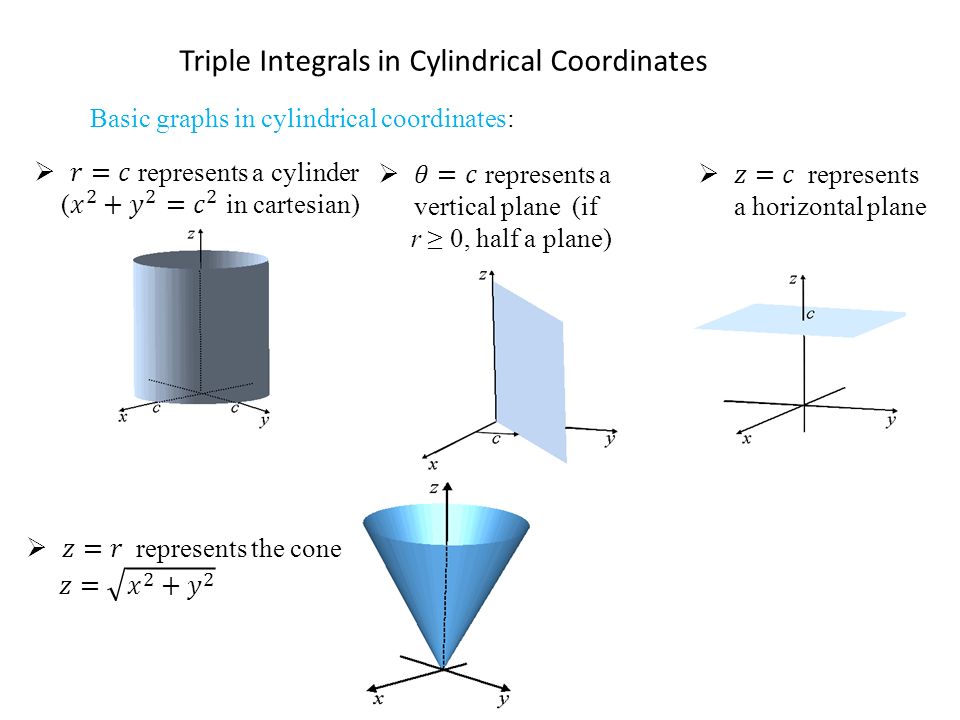
Triple Integral In Cylindrical Coordinates Ppt Video Online Download

Circle Equations

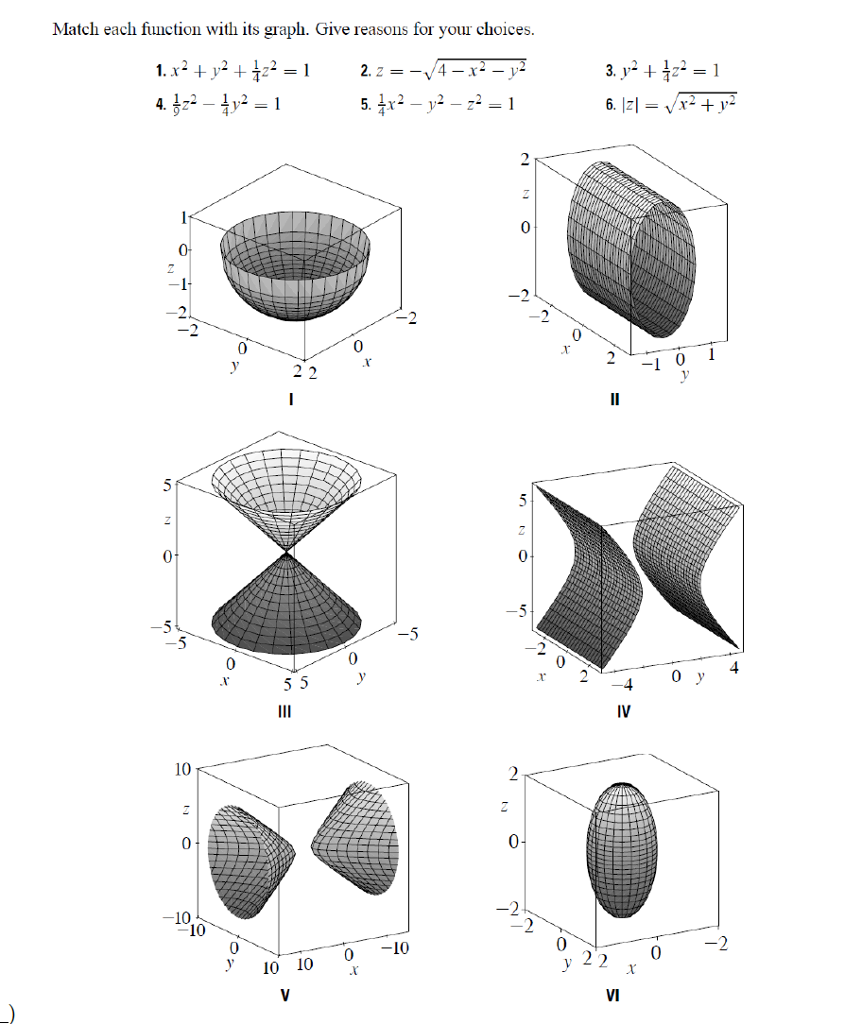
Solved Match Each Function With Its Graph Give Reasons For Chegg Com

What Is The Graph Of X 2 Y 3 X 2 2 1 Quora

1

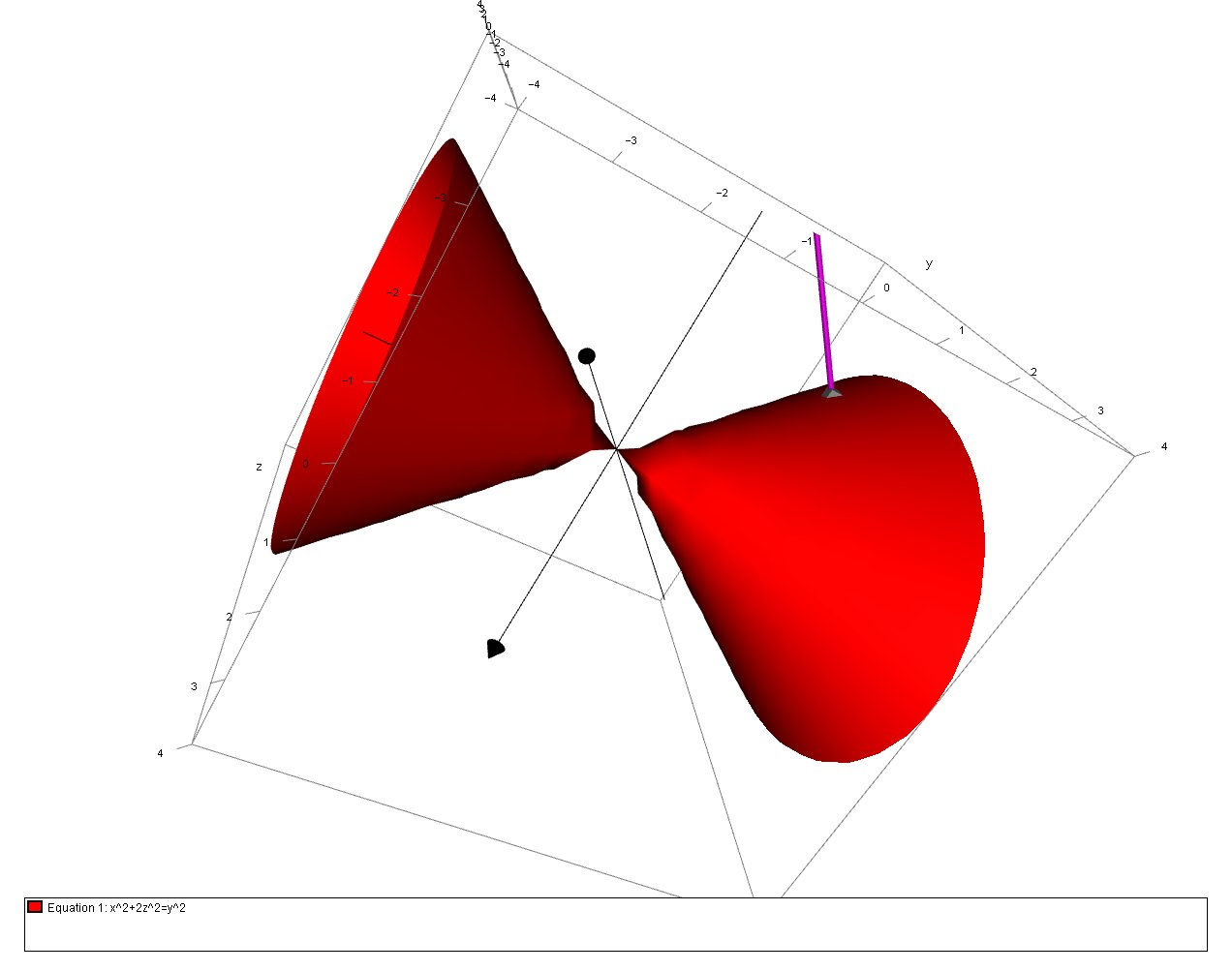
Solved Match The Equation With Its Graph Y2 X2 2z2 Chegg Com

How To Plot 3d Graph For X 2 Y 2 1 Mathematica Stack Exchange

23 Match The Equation X 2 Y 2 Z 2 1 With Its Graph Labeled I Viii Toughstem

15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts

X 2 Y 2 Z 2 R 2 Cardays

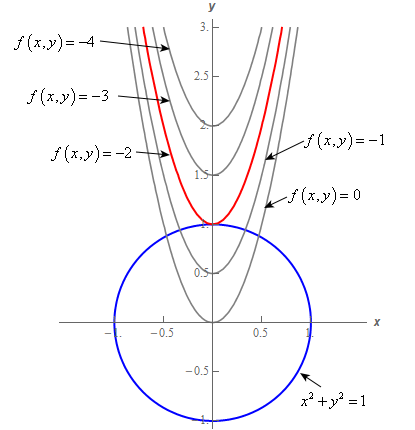
Calculus Iii Lagrange Multipliers

Surfaces Part 2

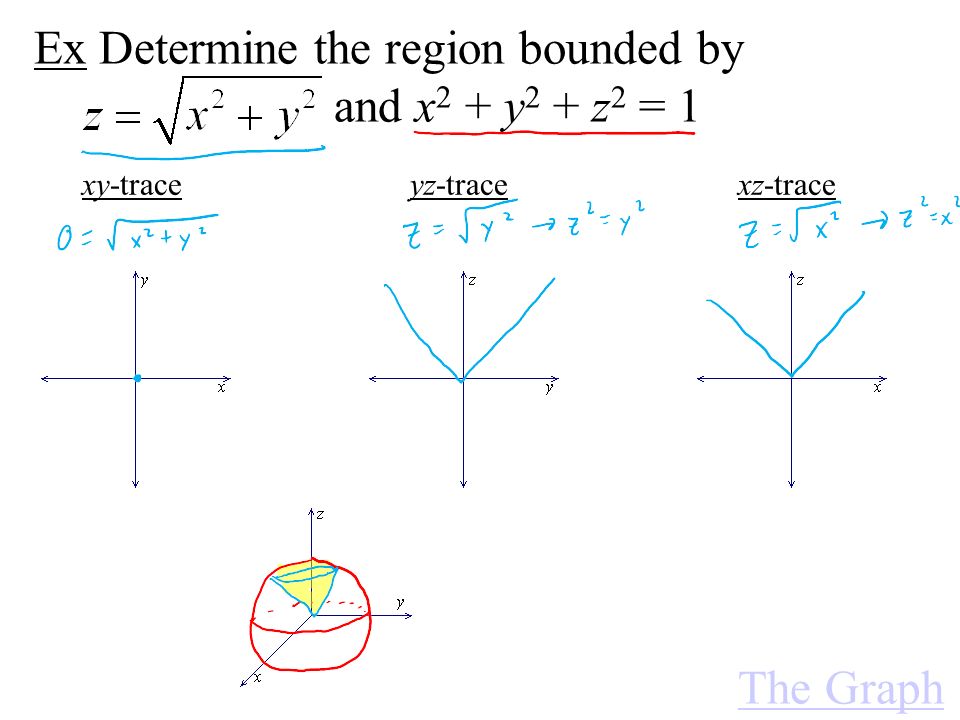
Cylinders And Quadratic Surfaces A Cylinder Is The Continuation Of A 2 D Curve Into 3 D No Longer Just A Soda Can Ex Sketch The Surface Z X Ppt Download

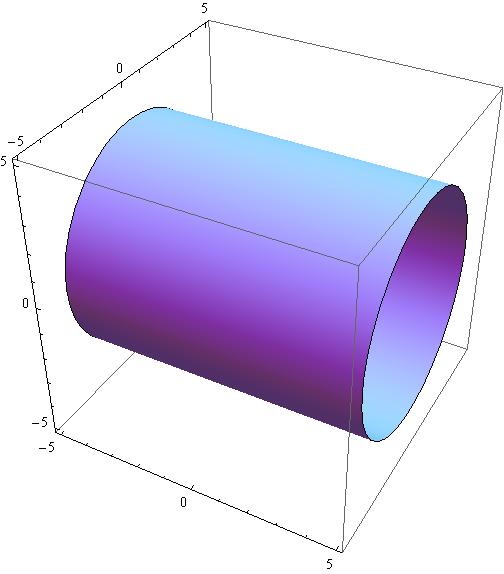
Y 2 Z 2 16 Is This Represents A Circle In 3 Dimensional Space Or 2 Dimensional Space Socratic

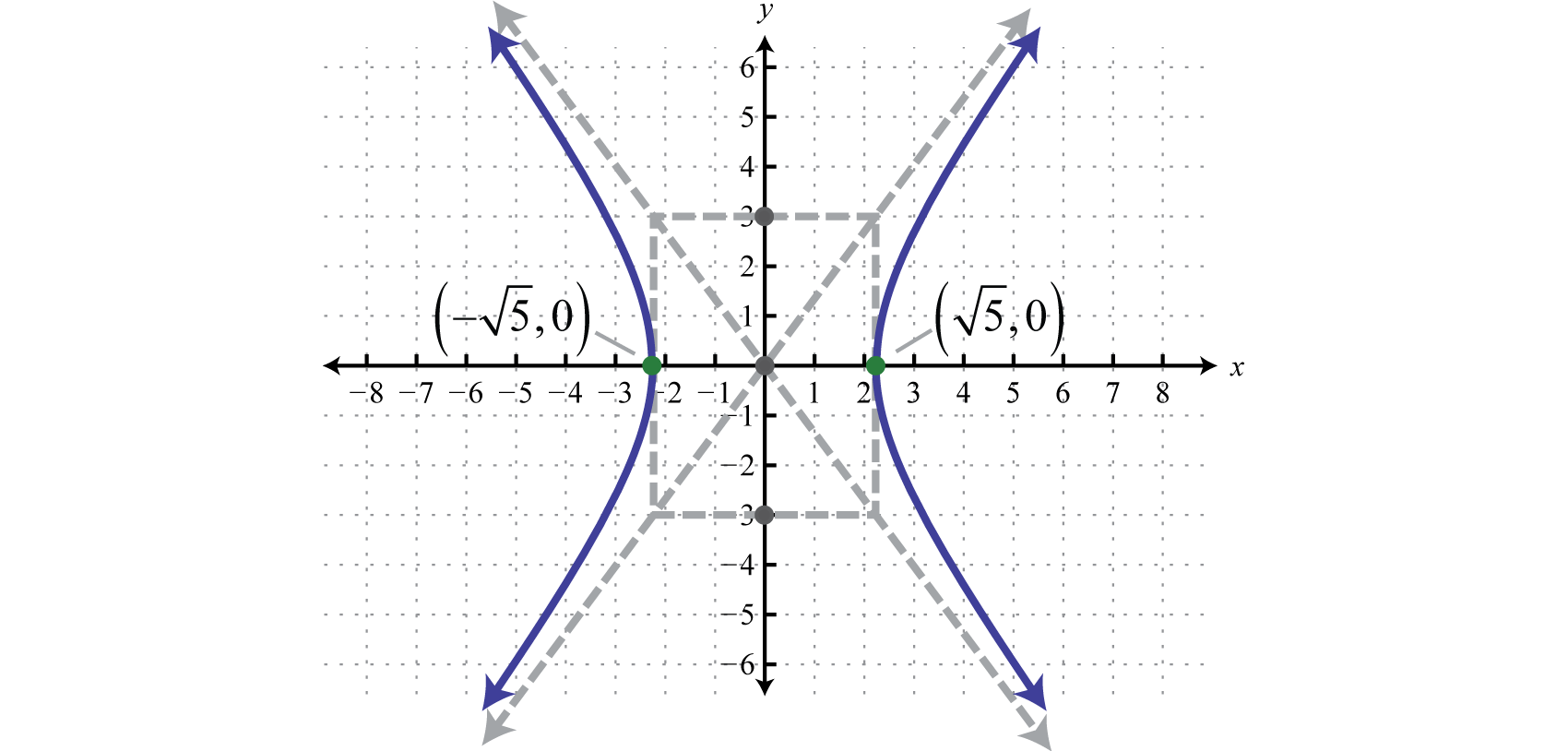
Hyperbolas

Graphs Root

Please Help Me Problem The Standard Form Of A Circle Is X H 2 Y K 2 R2 And Vertex Form For The Brainly Com

Surfaces Part 2

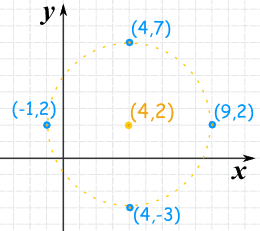
Circle Equations

Systems Of Equations With Graphing Article Khan Academy

Saddle Point Wikipedia

Complex Numbers Absolute Value

Graphing 3d Graphing X 2 Y 2 Z 2 Intro To Graphing 3d Youtube

Surface Area

印刷可能 X2 Y2 Z21 Graph シモネタ

Polar Html

Graph X 2 Ky 2 25 For Different Values Of K

Graph Pqr With Vertices P 2 3 Q 1 2 And R 3 1 And It S Image After The Translation X Y Brainly Com

Triple Integrals In Cylindrical And Spherical Coordinates

Digital Image Synthesis Yung Yu Chuang 10 4 Ppt Download

12 6 Quadric Surfaces Mathematics Libretexts

Double Integrals Volume And Average Value

Graphing Functions Of Two Variables By Openstax Jobilize

Double Integrals In Polar Coordinates Calculus Volume 3

1

Surfaces

Surfaces Part 2

How Do You Find The Equations For The Tangent Plane To The Surface X 2 2z 2 Y 2 Through 1 3 2 Socratic

16 2 Iterated Integrals Writing A Double Integral As An Iterated

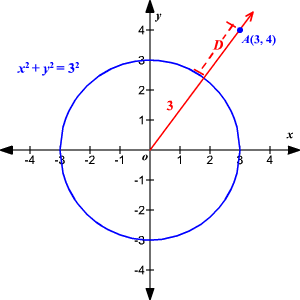
Shortest Distance Between A Point And A Circle

Describe Sketch And Name These Cylinders And Quadric Surfaces In R 3 A 4 X 2 16 Y 2 Z 2 16 B X 2 4 Y 2 4 Z 2 0 C X 2 Y 3 Z 12 D Y 2 Z 2 9 Study Com

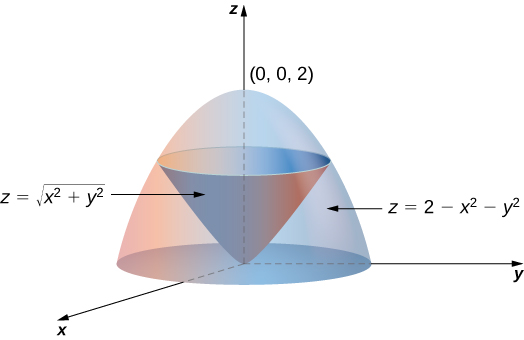
Triple Integrals In Cylindrical And Spherical Coordinates Calculus Volume 3

Graphing Inequalities X Y Plane Review Article Khan Academy

23 Match The Equation X 2 Y 2 Z 2 1 With Its Graph Labeled I Viii Toughstem

Cylindrical Coordinates In Matlab

Create A Contour Plot In Sas The Do Loop

2

Equation Of A Sphere Graph Physics Forums

How Should I Draw Graph Of Math X 2 Y 2 0 Math The Radius Is Zero What Should I Do Quora

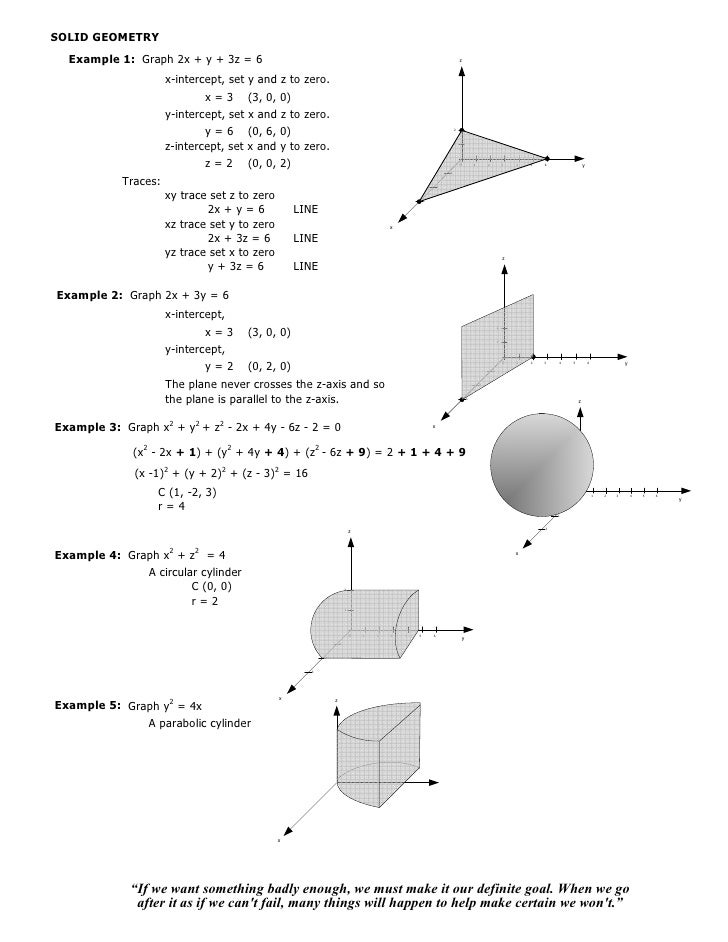
009 Solid Geometry

2

Surface Area

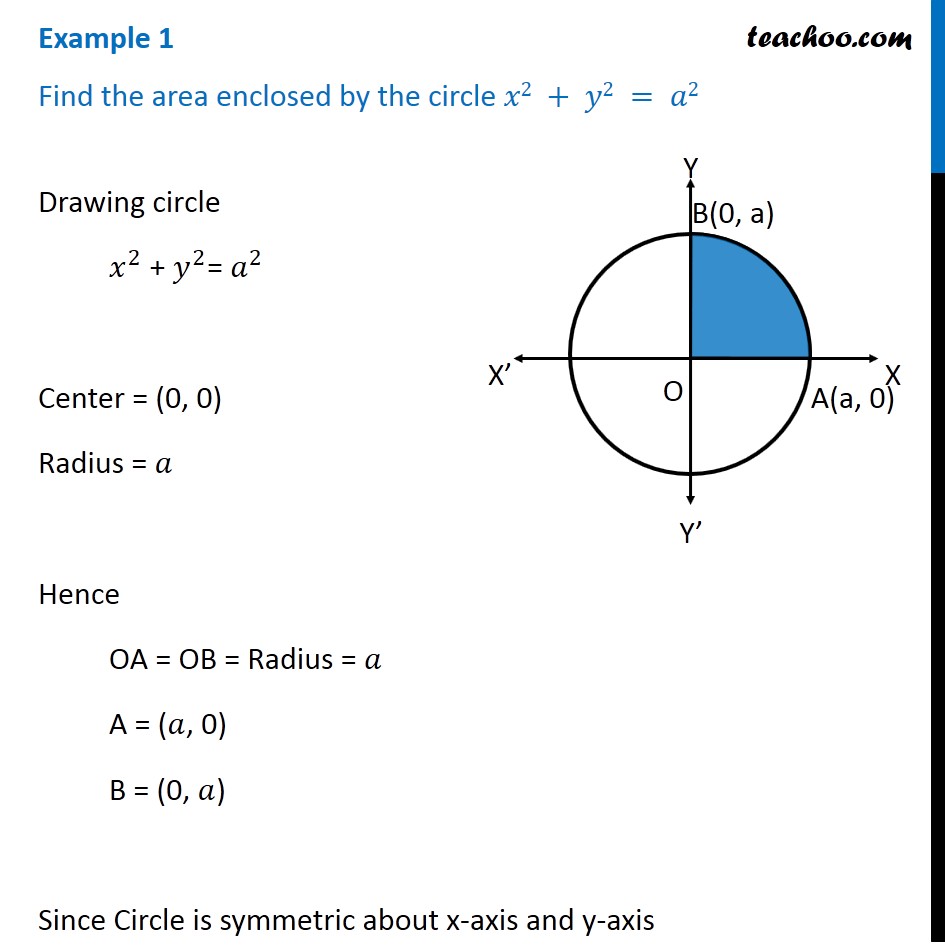
Example 1 Find Area Enclosed By Circle X2 Y2 Examples

Graph X 2 Y 2 4 Youtube

Parameterized Surfaces 2 Html

15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts

Section 9 1 Three Dimensional Coordinate Systems X 2 Y 2 Z Sx 2 Y 2 Z 2 2 Xy Plane It Is Sketched In Figure Pdf Free Download

Tgraph2d

Circle Equations

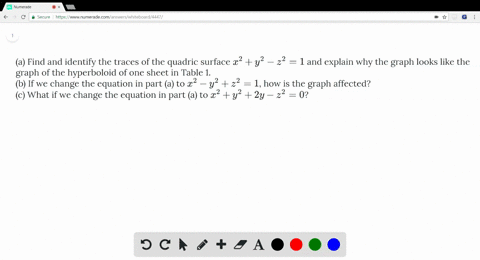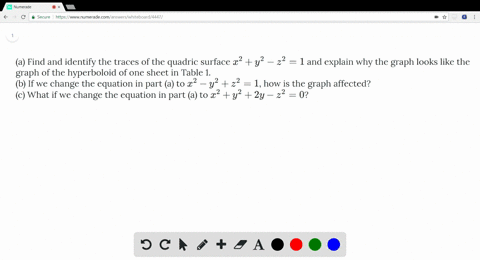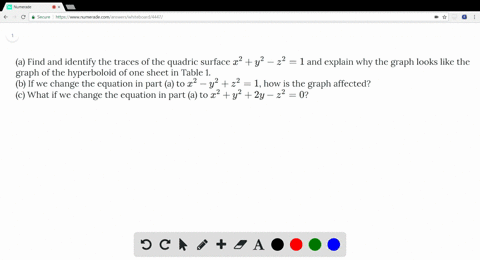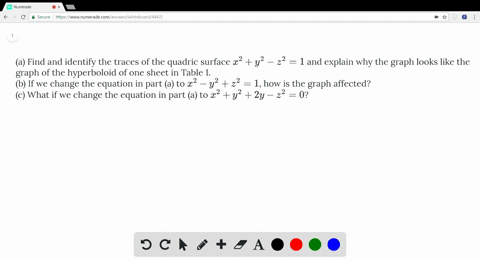
Solved A Find And Identify The Traces Of The Quadric Surface X 2 Y 2 Z 2 1 And Explain Why The Graph Looks Like The Graph Of The Hyperboloid Of One Sheet

Finding Volume Of Solid Under Z Sqrt 1 X 2 Y 2 Above The Region Bounded By X 2 Y 2 Y 0 Mathematics Stack Exchange

Surfaces Part 2

Surfaces

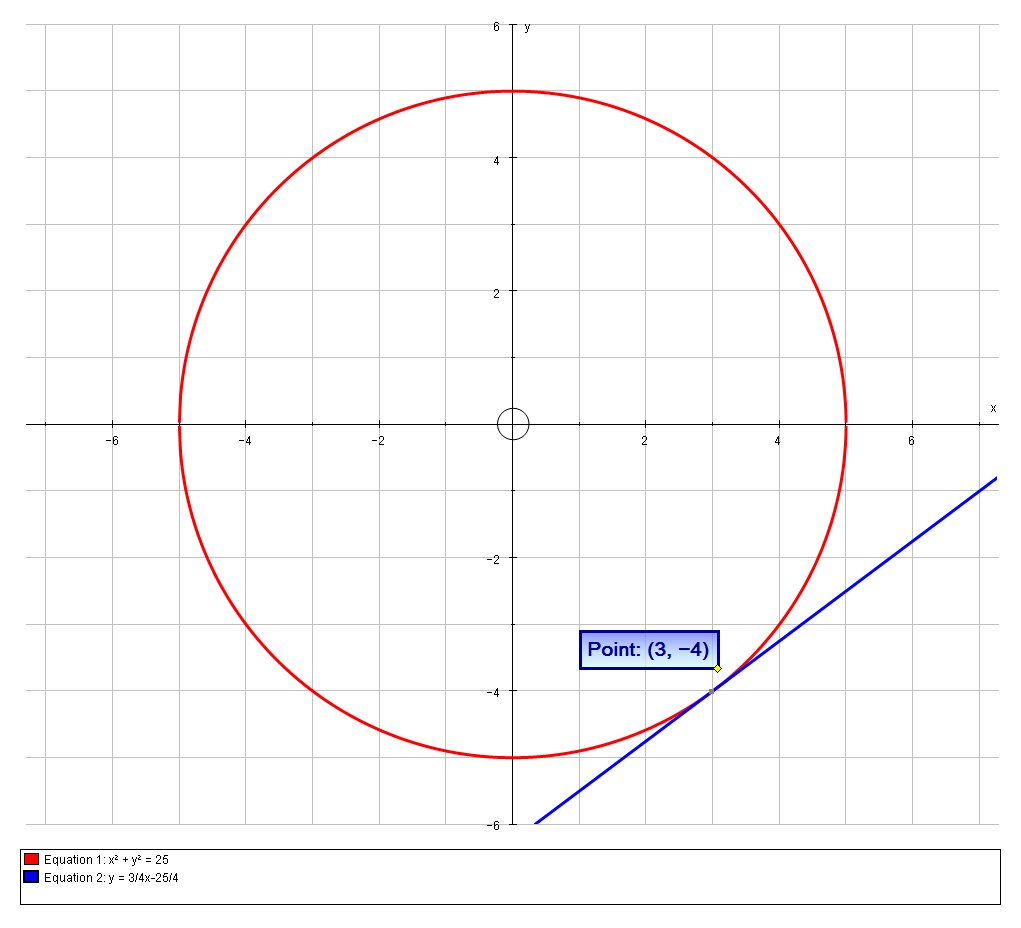
How Do You Find An Equation For The Line Tangent To The Circle X 2 Y 2 25 At The Point 3 4 Socratic

Introduction To Functions Of Several Variables Ppt Download

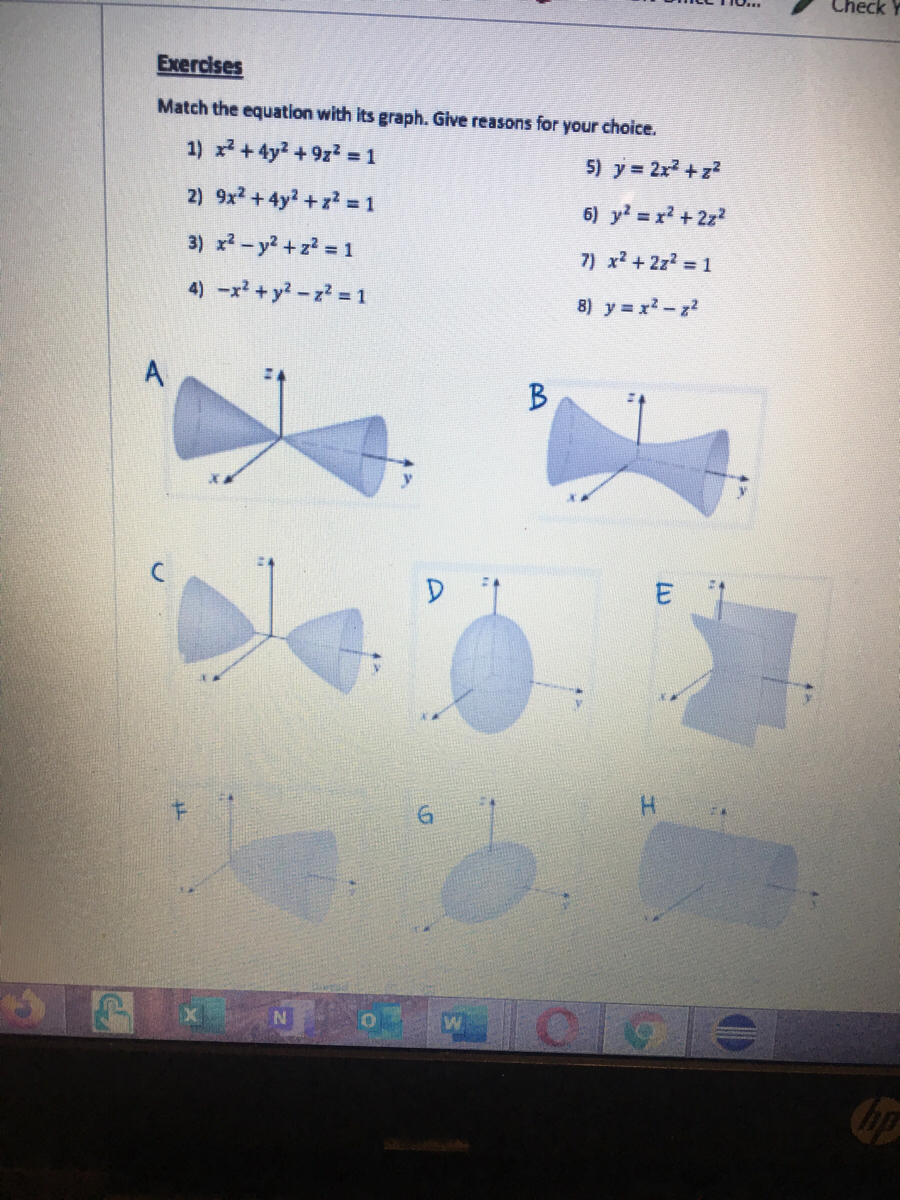
Answered Exercises Match The Equation With Its Bartleby

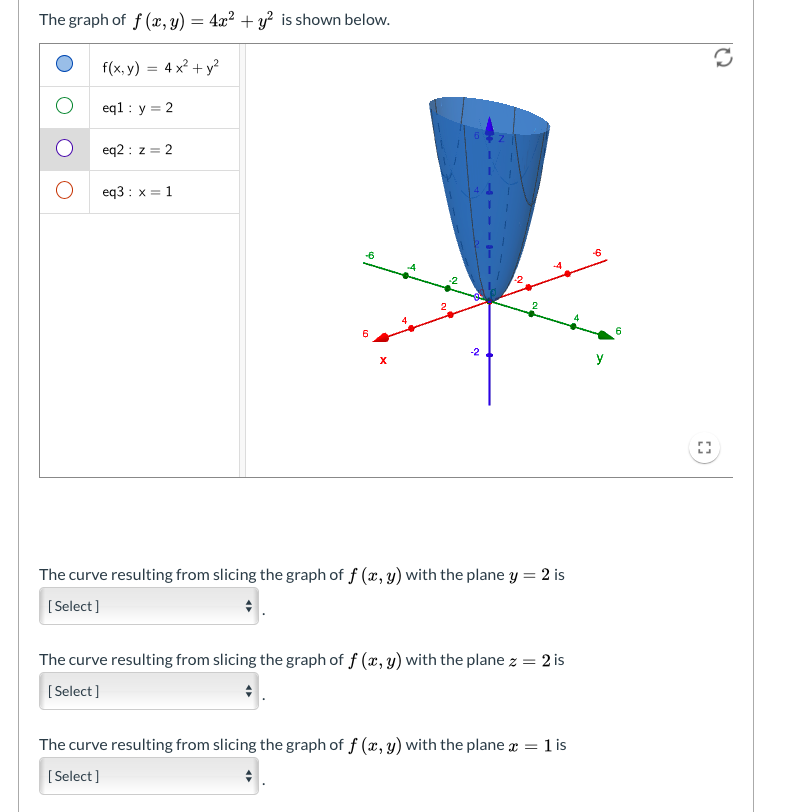
Solved The Graph Of F X Y 4 X2 Y2 Is Shown Below Chegg Com

Solved Match The Equation With Its Graph X2 Y2 Z2 1 R Chegg Com

What Is The Graph Of X 2 Y 2 Z 2 1 Quora