70以上 y(4x y)dx-2(x^2-y)dy=0 224240-Y(4x+y)dx-2(x^2-y)dy=0

0 votes 1 answer If π/2 < x < 0 and y = tan^1√((1 cos 2x)/(1 cos 2x)), find dy/dx asked in Differentiation by Kaina (305k points)If y = 5x3 4x and dx/dt= 2, find dy/dt when x = 3 dy dt = ?This is an example of a common AS differentiation Q To find dy/dx simply apply the power rule to each term in the equation The power rule is if you have a term x^n then dy/dx will be n times x^ (n1) eg for 4x^3 we multiply 3 by 4 for our coefficient and subtract 1 from the power giving us 12x^2 So here dy/dx = 12x^2 x^1/2

Solve The Differential Equations 2x Y 1 Dx 4x 2y 1 Dy 0 Sarthaks Econnect Largest Online Education Community

Y(4x+y)dx-2(x^2-y)dy=0

Y(4x+y)dx-2(x^2-y)dy=0-Science & Mathematics / Mathematics Please enter comments Kruger, Freddy Kruger May 21 0 Replies would yo pay 3160 for a 3 song cd which there areD dx (y) = d dx (4x3 x2 2 6) d d x ( y) = d d x ( 4 x 3 x 2 2 6) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps 12x2 x 12 x 2 x Reform the equation by setting the left side equal to the right side y' = 12x2 x y ′

How To Solve The Following Problem And What Type Of Equation Is It Quora

Get an answer for '`3(y4x^2)dx xdy = 0` Solve the firstorder differential equation by any appropriate method' and find homework help for other Math questions at eNotesA first order Differential Equation is Homogeneous when it can be in this form dy dx = F ( y x ) We can solve it using Separation of Variables but first we create a new variable v = y x v = y x which is also y = vx And dy dx = d (vx) dx = v dx dx x dv dx (by the Product Rule) Which can be simplified to dy dx = v x dv dxWhat is the general solution of y (4x y 2) dx (xy y) dy=0?

 If y = cos^–1(2x) 2cos^–1√(1 – 4x^2), 0 < x < 1/2 , find dy/dx asked in Limit, continuity and differentiability by Raghab (507k points) differentiation; #2 For the curve given by 4x2y2=4xy show that dy/dx=y4x/yx #3 For the curve given by 4x2y2=4xy, find the positive y coordinate given that the xcoordinate is 2 #4 For the curve given by 4x2y2=4xy, show that there is a point P with xcoordinate 2 at which the line tangent to the curve at P is horizontalFull access to over 1 million Textbook Solutions;

You can separate it out as xdxydy = x2−1y21 now put y2 1 = u and then continue to get a very simple integrable function 21 (xy2x)dx (yx2y)dy=0 One solution was found d = 0 Step by step solution Step 1 Step 2 Pulling out like terms 21 Pull out like factors y Is the solution of the math problem right? Example 22 Find the particular solution of the differential equation 𝑑𝑦/𝑑𝑥𝑦 cot⁡〖𝑥=2𝑥𝑥^2 cot⁡𝑥(𝑥≠0) 〗 given that 𝑦=0 𝑤ℎ𝑒𝑛 𝑥=𝜋/2 𝑑𝑦/𝑑𝑥𝑦 cot⁡〖𝑥=2𝑥𝑥^2 cot⁡𝑥 〗 Differential equation is of the form 𝑑𝑦/𝑑𝑥𝑃𝑦=𝑄 where P = cot x & Q = 2x x2 cot x IF = 𝑒^∫1 〖𝑝 𝑑𝑥Int (((xy)/2)^2 (1(xy)/2)^2) dx dy, x=0 to 1, y=0 to 1 Natural Language;

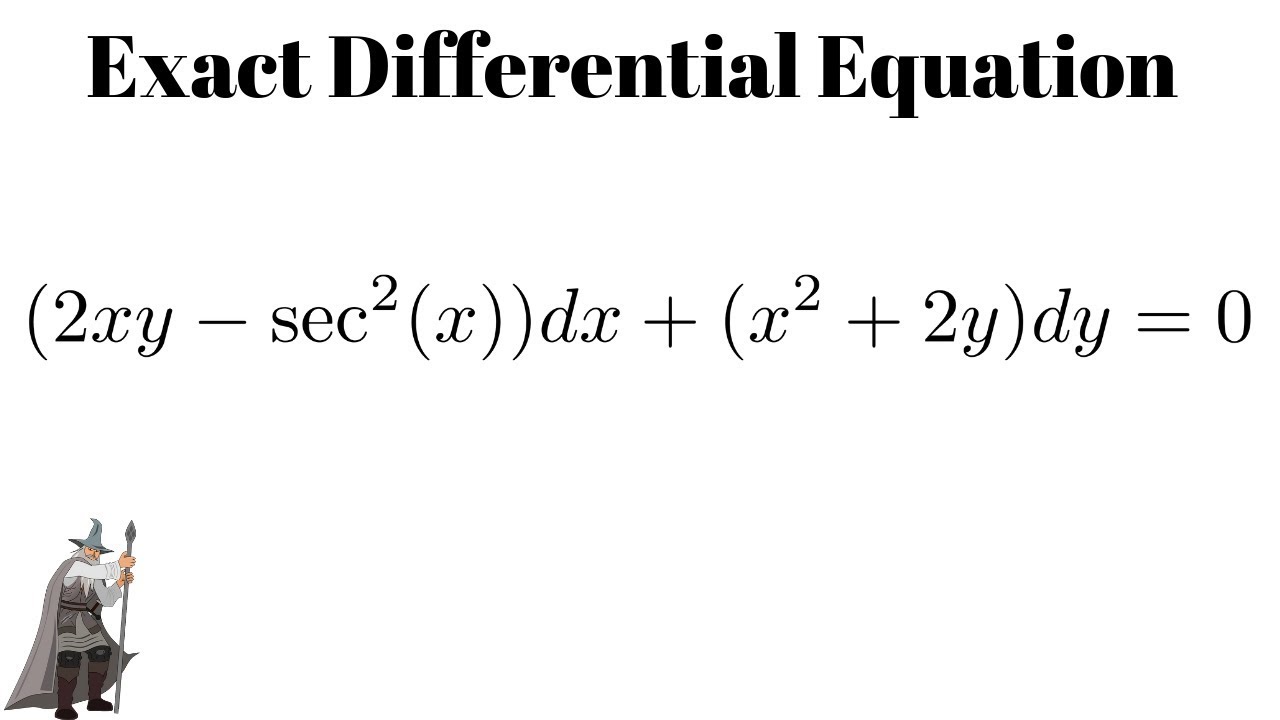
Exact Differential Equation 2xy Sec 2 X Dx X 2 2y Dy 0 Youtube

Math 432 Hw 2 5 Solutions Pdf Free Download

Solution Verified by Toppr (x 2−y 2)dx−xydy= dxdy= xyx y Let y=vx, dxdy=vx dxd dd d d = dx 4−1ln(1−2t)=lnx 4lnxln(1−2t)c=0 lnx 4ln(1−2v 2)c=0 lnx 4ln(1−2 x 2y 2)c=0 lnx 4ln(x 2−2y 2)−ln(x) 2c=0 lnx 2ln(x 2−2y 2)c=0 2lnxln(x 2−2y 2)c=0 Solve any question of Differential Equations with Patterns of problems > Was this answer helpful?4 The integrating factor of the differential equation x dy x 2y=x2 x d y x 2 y = x 2 is (x≠ 0) ( x ≠ 0) Answer 5 The number of solutions for the equation Sin2xCos4x=2 S i n 2 x C o s 4 x = 2 is Answer 6 The curve satisfying the differential equation, (x2 −y2)dx2xydy=0 ( x 2 − y 2) d x 2 x y d y = 0 and passing through Explanation First, we are going to divide the entire equation by x to put it into the form dy dx P (x)y = Q(x) dy dx 2 x y = xlnx Now, we need to find the special integrating factor For a differential equation in this form, the special integrating factor is given by μ = e∫P (x)dx μ = e∫ 2 xdx μ = e2lnx

What Is The Solution To 2y 3x Dx 4xy Dy 0 Solucao Geral Da Edo Quora

The Solution Of 2 X 2 Y 2 Dx 4xy Dy 0

Y x)dx (x² – 2)dy = 0 4 y (4x y)dc 2 (x2 y)dy = 0 5 (4xy 3y2 x)dx x (x 2y)dy = 0 Expert Solution Want to see the full answer?Solution for (x y) (4x y) dx x(5x y) dy = 0 Q If sin a = 0784 and sin 8 = 0577 with both angles' terminal rays in QuadrantI, find the A sinα = 0784 sinβ = 0577 sin(βα ) = sinαcosβ cosαsinβ cos(αβ) = cosαcosβ sinαsinβ use thisSteps Using the Quadratic Formula Steps for Completing the Square View solution steps Graph Quiz Linear Equation y(4x y)dx− 2(x2y− y)dy = 0 Similar Problems from Web Search finding y (xy2 y)dx (x2y −x)dy = 0 https//mathstackexchangecom/questions//findingyxy2ydxx2yxdy0/

Solve The Differential Equations 2x Y 1 Dx 4x 2y 1 Dy 0 Sarthaks Econnect Largest Online Education Community

What Is The Solution To X 2xy Y Dx 2x Y 4xy Sin Y Dy 0 Quora

3 Rate of Change To work out how fast (called the rate of change) we divide by Δx Δy Δx = f (x Δx) − f (x) Δx 4 Reduce Δx close to 0 We can't let Δx become 0 (because that would be dividing by 0), but we can make it head towards zero and call it "dx" Δx dx You can also think of "dx" as being infinitesimal, or infinitely smallLimit of x^2 y^2 x y^3 as y > infinity int (x^2y^2)/ (x^2y^2) dxdy, int (x^2y^2)/ (x^2y^2) dydx Jacobian series of x^2 y^2 x y^3 at y=0 ʃʃʃ exp (x y z) dx dy dz Have a question about using WolframAlpha?Use a substitution to replace the quantity squared Let and This is a separable ODE Form the two integrals and solve them The remaining integral requires a trigonometric substitution Continue Reading Sponsored by Cuemath Almost 75% of Cuemath students nailed this answer vs noncuemath students

Solved Find The Particular Solution Of Y 2x 2 Xy Y 2 Dx X 2 2x 1 Dy 0 Course Hero

Solved Consider The Differential Equation 3y 4xy 2 Dx 2x 3x 2 Y Dy Course Hero

Find dy/dx x^24xyy^2=4 x2 − 4xy y2 = 4 x 2 4 x y y 2 = 4 Differentiate both sides of the equation d dx (x2 −4xy y2) = d dx (4) d d x ( x 2 4 x y y 2) = d d x ( 4) Differentiate the left side of the equation Tap for more steps −4xy' 2yy' 2x−4y 4 x y ′ 2 y y ′ 2 x 4 y Since 4 4 is constant with respectHow do I solve dy/dx= (4xy1) ²?Give the BNAT exam to get a 100% scholarship for BYJUS courses

Special Integrating Factors For Solving Differential Equation Wy 2 2y 4x 2dx 2xy Xdy 0 Youtube

If Sin Y Dy Dx Cos X 2cos Y Sin 2x And Y 0 Pi 2 Then 198 E 2 4cos Y Pi 2 Is Equal To

What is the general solution of the ODE below Solve the ODE using Method of Grouping remove the factor Now, distribute the differentials and try to group by derivative rules The mixed terms have to be grouped together to match derivative rulesCheck out a sample Q&A here See Solution star_border Students who've seen this question also like Given Curves y = 4x, x y = 3 , y = 0 and y=2 To find (x2 y2) dx dy throughout the area enclosed Solution Consider a strip parallel to x axis To calculate double integral, Think about the volume under a surface with condition z = f (x, y)

Solved Can You Answer For Me Thanks Course Hero

Can You Help Me How Do I Solve Y Y 2x 2 Dx 2 Y Dy 0 Quora

3) If x and y are in X, then f(x) = f y(4xy) dx 2(x^2y) dy =0 Solve this give me explanation and Get more out of your subscription* Access to over 100 million coursespecific study resources;Contact Pro Premium Expert Support » Give us your feedback »

Math 432 Hw 2 5 Solutions

Example 21 Find General Solution Ydx X 2y2 Dy 0

Here, ∂ M ∂ y = ∂ N ∂ x Thus the equation is exact ∴ ∫ M d x = ∫ x 2 − 4 x y − 2 y 2 d x = x 3 3 − 4 x 2 2 y − 2 y 2 x And ∫ terms in N free of x d y = ∫ y 2 d y = y 3 / 3 ∴ The solution is x 3 3 − 2 x 2 y − 2 x y 2 y 3 3 = c Get an answer for 'Let y=2(x^2)4x3 Find the differential dy when x=4 and dx=03Find the differential dy when x=4 and dx=06' and find homework help for other Math questions at eNotesSee the answer Solve y (4xy)dx 2 (x^2y)dy = 0 by finding the integrating factor and test for exactness Expert Answer 100% (1 rating) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator

Solve The Following X 2 4xy 2y 2 Dx Y 2 4xy 2x 2 Dy 0

What Is The General Equation Of Differential Equation Ydx X 2y Dy 0 Quora

 5 Here is another way y ( y 2 x 2) d x x ( 2 x 2 − y) d y = 0 Substitute y = t x t ( t 2 x) = ( t − 2 x) y ′ Note that y ′ = t ′ x t t ( t 2 x) = ( t − 2 x) ( t ′ x t) After some simplifications you get t ′ ( t − 2 x) = 4 tFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep Homework Statement I'm asked to use the transformation of v= 2xy to solve dy/dx = (2xy4)/ (4x2y 1) the answer given is (2/9)(6x3y2) Insights Blog Browse All Articles Physics Articles Physics Tutorials Physics Guides Physics FAQ Math Articles Math Tutorials Math Guides Math FAQ Education Articles Education Guides Bio/Chem

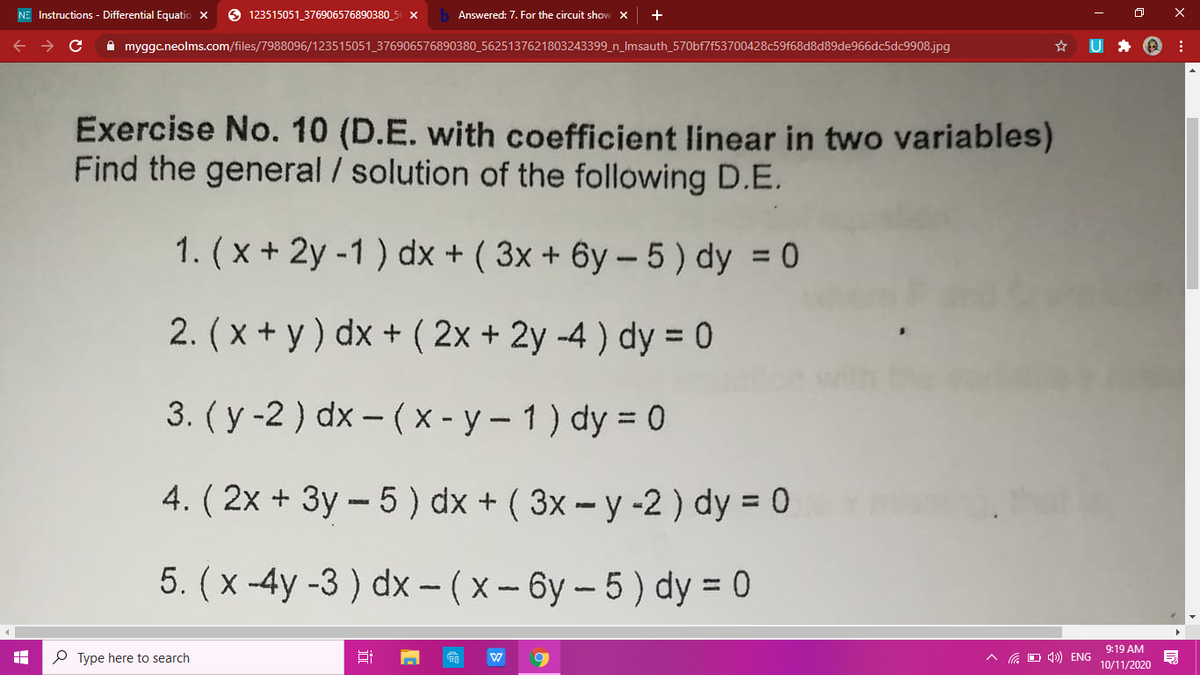
Answered X Y Dx 2x 2y 4 Dy 0 3d Bartleby

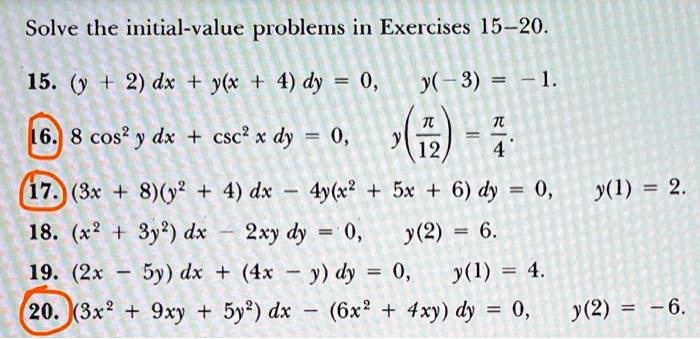
Solved Solve The Initial Value Problems In Exercises 15 15 Y 2 Dx L 4 Dy 0 Y 3 4 16 8 Cos Y Dx Csc X Dy 0

The differential equation of the form is given as d y d x = x y 2 Separating the variables, the given differential equation can be written as 1 y 2 d y = x d x ⇒ y – 2 d y = x d x – – – ( i) In the separating the variables technique we must keep the terms d y and dY)dx %3D 2 xy2 dx x²ydy = 0 3 2y (x?Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep

Solve The Differential Equation Dy Dx Square 4x Y 1 Youtube

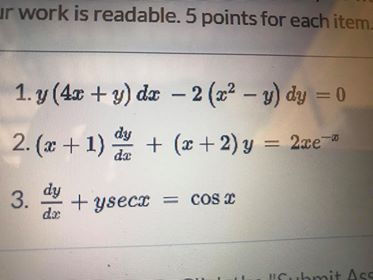
Solved Ur Work Is Readable 5 Points For Each Item 1 Y 4x Chegg Com

Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics2) If x and y are in X, then f(x) = y;This problem has been solved!

What Is The Solution For Y 4xy 4x 2 3 Y Xe X 2 Where Y 0 0 Y 0 1 Quora

How To Solve This Differential Equation Y Xy 2 Dx X X 2 Y 2 Dy 0 Quora

In mathematics, a function (or map) f from a set X to a set Y is a rule which assigns to each element x of X a unique element y of Y, the value of f at x, such that the following conditions are met 1) For every x in X there is exactly one y in Y, the value of f at x; Given (y − 4x −1)2dx − dy = 0 dy dx = (y − 4x −1)2 Let u = y −4x, then du dx = dy dx −4 du dx 4 = (u − 1)2 du dx = u2 −2u −3 The equation is separable du u2 − 2u − 3 = dx ∫ du u2 − 2u −3 = ∫dx24/7 help from Expert Tutors on 140 subjects;

How To Solve Show The Differential Equations Are Exact 2xy Y Tany Dx X 2 X Tany 2 Secy 2 2 Dy 0 Te Tx 2x Dx Dt Xe Xt 0 Quora

Solved Determine Which Equations Are Exact And Solve Them Chegg Com

 Misc 13Find a particular solution of the differential equation 𝑑𝑦﷮𝑑𝑥﷯𝑦 cot﷮𝑥=4𝑥 𝑐𝑜𝑠𝑒𝑐 𝑥 𝑥≠0﷯ ,﷯ given that 𝑦=0 when 𝑥= 𝜋﷮2﷯Given 𝑑𝑦﷮𝑑𝑥﷯𝑦 cot﷮𝑥=4𝑥 𝑐𝑜𝑠𝑒𝑐 𝑥 ﷯This of the form 𝑑𝑦﷮𝑑𝑥﷯𝑃𝑦=𝑄 where P = cot x & Q = 4x cosec xIF = 𝑒﷮ ﷮﷮𝑃𝑑𝑥﷯﷯IFGiven that y = 4x^3 – 5/ (x^2) , x =/= 0, find in its simplest form dy/dx We are given y = 4x^3 – 5/ (x^2) To find the dy/dx we are going to use the power rule, from the power rule differentiating x^n gives n*x^n1, so from our equation differetiating x^3 will give 3x^2, but we need the differential of 4x^3, this will be 12x^3Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

Solved I Linear Equation Of Order One 1 Xdy Y Xy 2 Dx Chegg Com

How To Solve The Following Non Homogenous Differential Equation Dy Dx 4x 3y 15 2x Y 7 Quora

SolutionGiven , Differential Equation is(x 2−yx 2)dy(y 2xy 2)dx=0This can be Simplified as(yx 2−x 2)dy=(y 2xy 2)dxx 2(y−1)dy=y 2(1x)dxy 2dy(y−1)= x 2dx(1x)Now On Integrating both side , we get∫ y 2dy(y−1)=∫ x 2dx(1x)∫y1− y 21dy=∫x1 x 21dx∫ ydy− y 2dy=∫ xdx x 2dxln∣y∣− y1=ln∣x∣− x1lnCln∣yTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `x(1y^2)dxy(1x^2) dy=0` Best answer Answer is (A), (D) See fig The given differential equation is x2 4x 4 y (x 2)dy/dx y2 = 0 (x > 0) which is further simplified as follows (x 2)2 y (x 2)dy/dx y2 = 0 Substituting x 2 = t, we get dx/dy = dt/dy which passes through the point (1, 3) Therefore, from Eq (1), we get

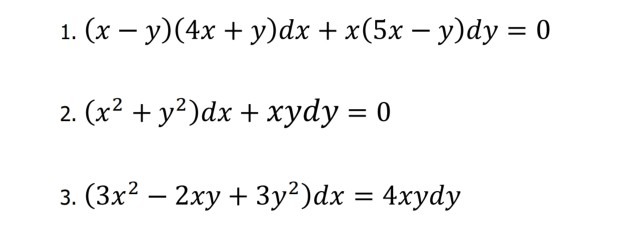
Solved 1 X Y 4x Y Dx X 5x Y Dy 0 2 X2 Y2 Dx Chegg Com

How Would You Solve 3x 2y 5 Dx 2x 3y 7 Dy Quora

Solve the following differential equations 1 xdy = (xy? Solve the problem dy/dx = sin(4x) / 3cos(4x) y=5 when x=0 2 (i)Show that ∫ 2e^2x – 5 / (e^2x – 5x) ^2/3 dx = 3(e^2x – 5x)^1/3 c where c is the arbitrary constant (ii)Hence find,The general solution of the differential equation is of the form f (x,y)=C f (x,y) = C \frac {dy} {dx}=\frac {3x^24x2} {2\left (y1\right)} dxdy = 2(y 1)3x2 4x2 3 Using the test for exactness, we check that the differential equation is exact 0=0 0 = 0 Explain more 4 Integrate M (x,y) M (x,y) with respect to x x to get

Solved Exercises Obtain Family Of Solutions 1 X 2y Dx 2x Y Dy 0 2 2 2x2 Y2 Dx Xydy 0 3 Xydx X2 3y2 Dy 0 4 Xy

Solved Q 1 A Solve The Differential Equation By Exact Equation Method 3x2 4xy Dx 2x2 2y Dy Given That Y 0 When X 0 Marks B Find The General

⇒ y4x−4 =2 ⇒ y 4 x − 4 = 2 tan (2x) ( 2 x), which is required solution Concepts Used General Solutions to Differential Equations A relation between involved variables, which satisfy the given differential equation is called its solution

Solved Solve The Following Differential Equations Question Chegg Com

Solved Check If The Given Answers Are Correct Or Not Chegg Com

Answered 4 Y 4x Y Dc 2 X2 Y Dy 0 Bartleby

How To Solve X Y Dx 2xy Dy 0 Quora

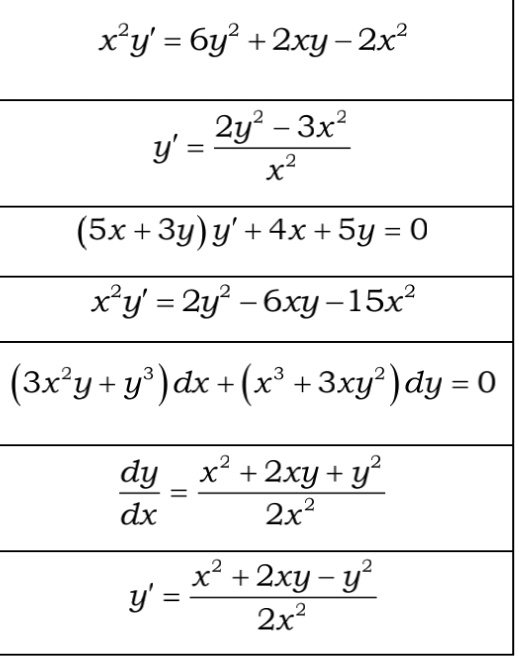
Solved Xly 6y2 2xy 2x2 2y2 3x2 Y T Sx 3y Y 4x Sy 0 Xy 2y 6xy 15x2 3xy Y Dx X 3xy Dy 0

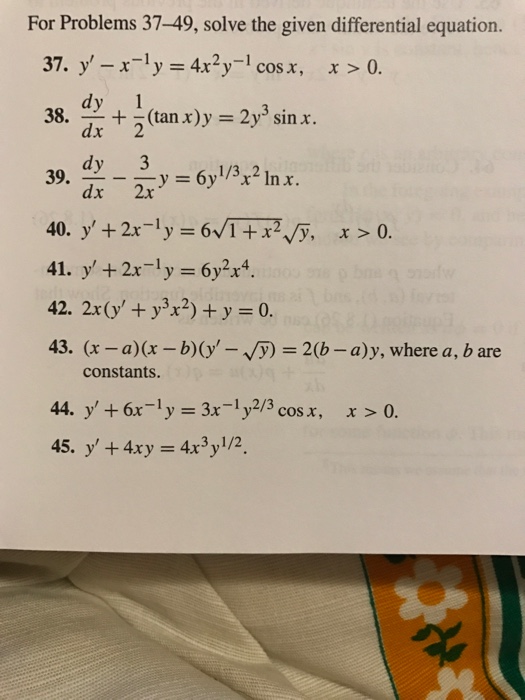
Solve The Given Differential Equation Y X 1 Y 4x 2y 1 Cos X X 0 Dy Dx 1 2 Tan X Y 2y 3 Sin X Dy Dx 3 2x Y 6y 1 3 X 2 Ln

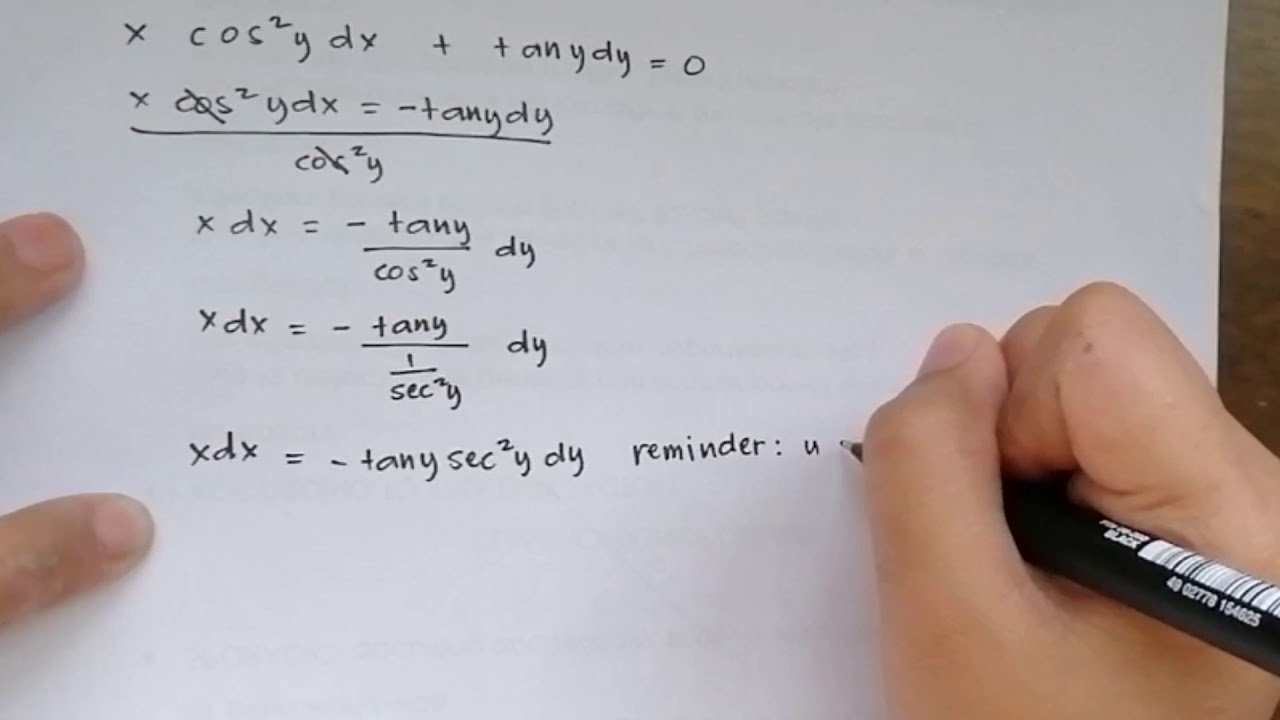
Xcos 2 Y Dx Tan Y Dy 0 Youtube

Engineering Mathematics Notes

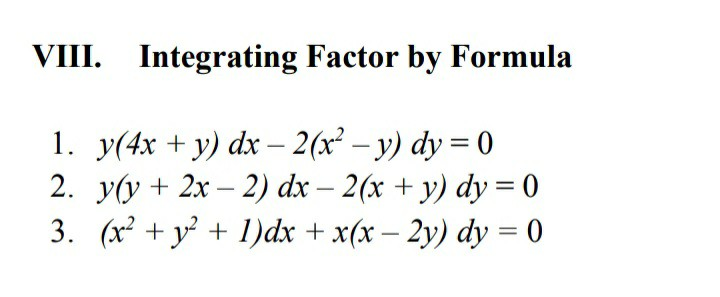
Solved Viii Integrating Factor By Formula 1 Y 4x Y Dx Chegg Com

Engineering Mathematics Notes

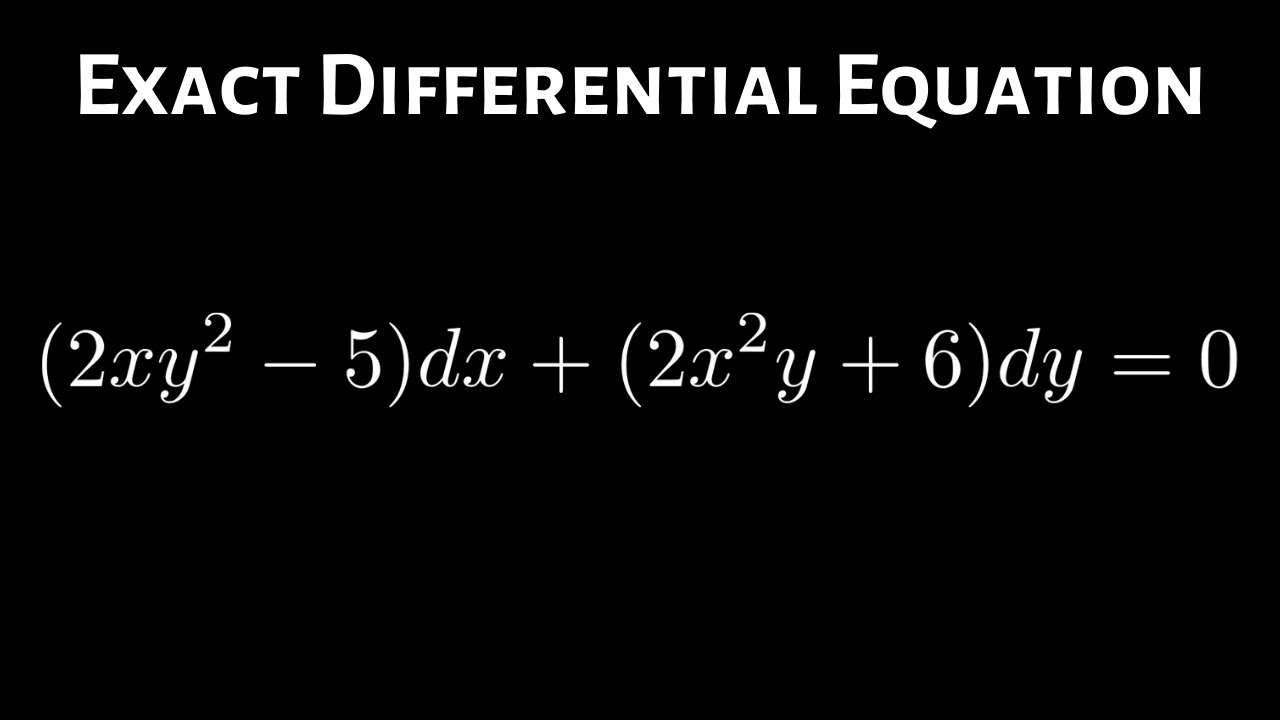
Exact Differential Equation 2xy 2 5 Dx 2x 2y 6 Dy 0 Youtube

X Y 4x Y Dx X 5x Y Dy 0 Youtube

Solve The Following Ordinary Differential Equation 2y 2 2y 4x 2 Dx 2xy X Dy 0 Wegglab

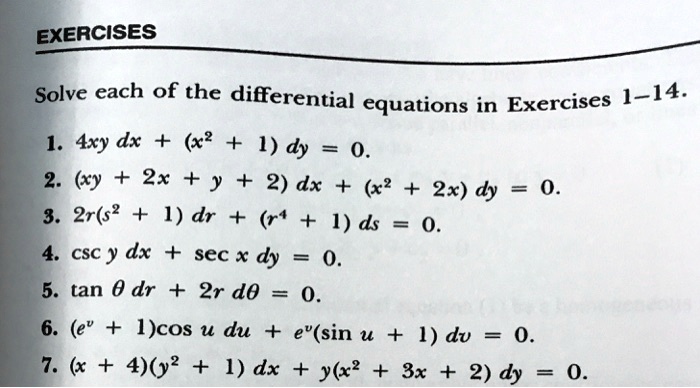
Solved Exercises Solve Each Of The Differential Equations In Exercises 1 14 1 4xy Dx 1 Dy 0 2 Xy 2x Y 2 Dx 2x

For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube

Solve The Following Differential Equations 1 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Youtube

Solved In Problems 31 Through 42 Verify That The Given Chegg Com

Solved Set Of Solutions Unless The Statement Of The Exercise Stipulates Otherwise In Each Exercise Find Y2 3y X Dx 2y 3 Dy 0 Y Y I Dx Xk

Solved Find A Set Of Solutions To The Following Differential Equations 1 X Y 4x Y Dx X 5x Y Dy 0 2 X Ylny Y In X D Course Hero

Solved Exercises Solve Each Of The Differential Equations In Chegg Com

I The Degree Of The Differential Equation D 2 Y Dx 2 E Dy Dx 0 Is Ii The Youtube

What Is Solution Of Cosec Y Dx Sec X Dy 0 Quora

Solved Pertormance Task Solve For The General Solution Part I Homogeneous De X Y Dx X Y Dy 0 2 3x 4y Dx 4x 3y Dy 0 Part 2

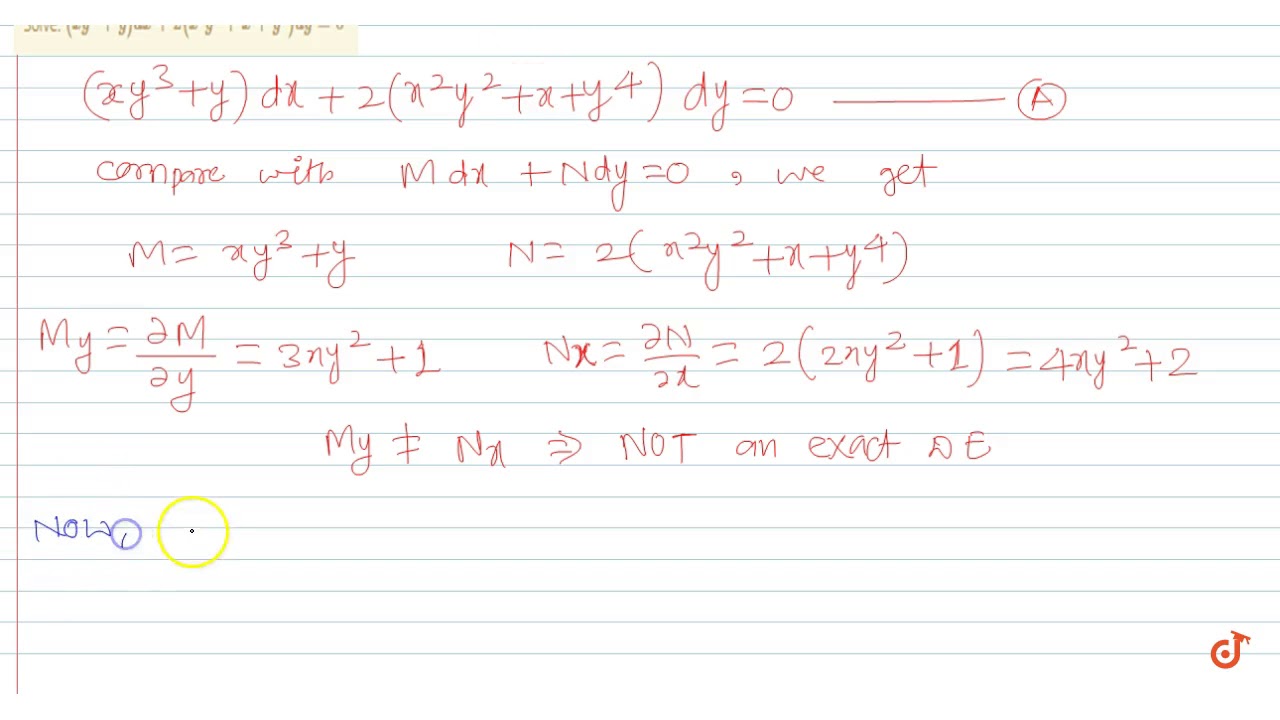
Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube

Differential Equations Practice 76 Y 1 Dx 4x Y Dy 0 Youtube

Solved Determination Of Integrating Factors Y Y 2x 2 Dx Chegg Com

How To Solve The Differential Equation X 4y 9 Dx 4x Y 2 Dy 0 Using Substitution Quora

Solved Thankyouuuu Course Hero

What Is The General Solution Of The Following First Order Odes Dy Dx 4x 3y 15 2x Y 7 Quora

Solved Solve The Differential Equation 2x Y Dx 4x 2y Chegg Com

Solved Y 4x Y Dx 2 X 2 Y Dy 0 Solve This Give Me Explanation And Course Hero

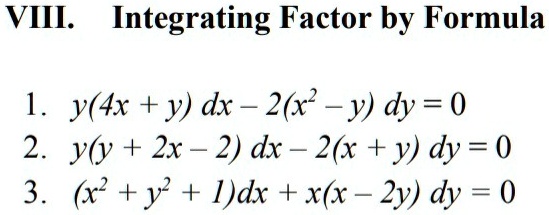
Solved Viii Integrating Factor By Formula 1 Y 4x Y Dx 2x Y Dy 0 2 Y Y 2x 2 Dx 2 X Y Dy 0 3

Solved Find The Solution Of The Following Differential Equations Show Your Solution Completely And Box Your Final Answer Submit Your Work Via File Upload In Pdf Format Make Sure Your Work Is

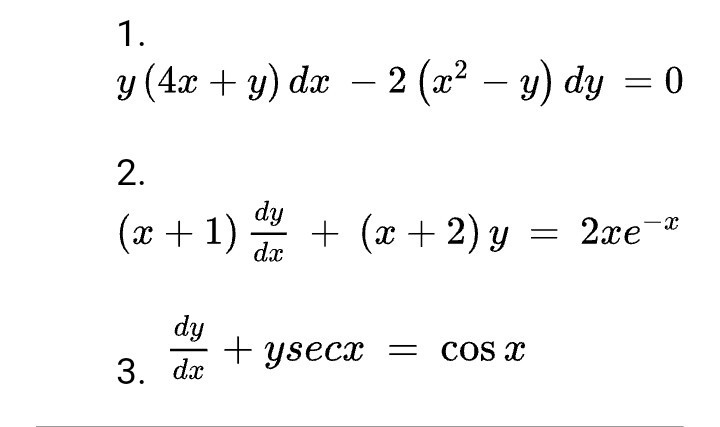
Solved 1 Y 4x Y Dx 2 X2 Y Dy 0 2 X 1 X 2 Chegg Com

Solved Obtain The Particular Solution Satisfying The Initial Chegg Com

Solved 4 Determine Whether The Equation Is Exact Otherwise Find An Integrating Factor Then Solve The Non Exact Equation Course Hero

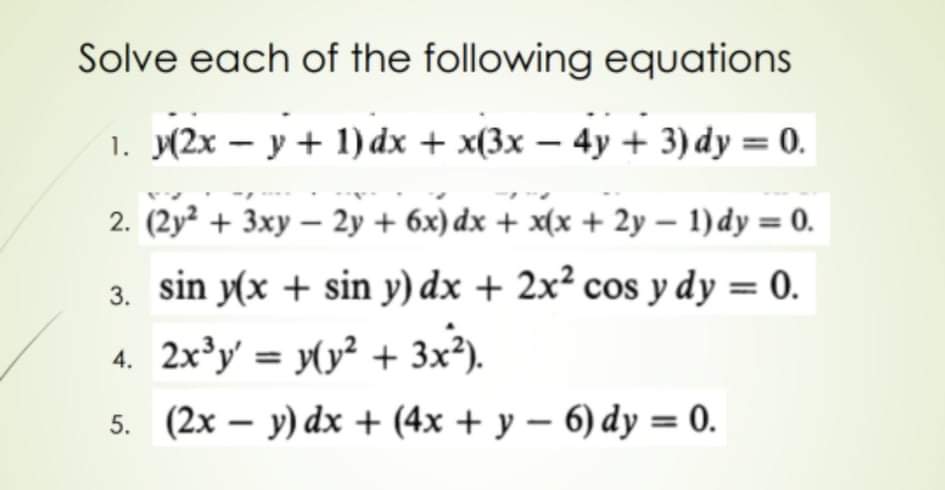
Answered 5 2x Y Dx 4x Y 6 Dy 0 Bartleby

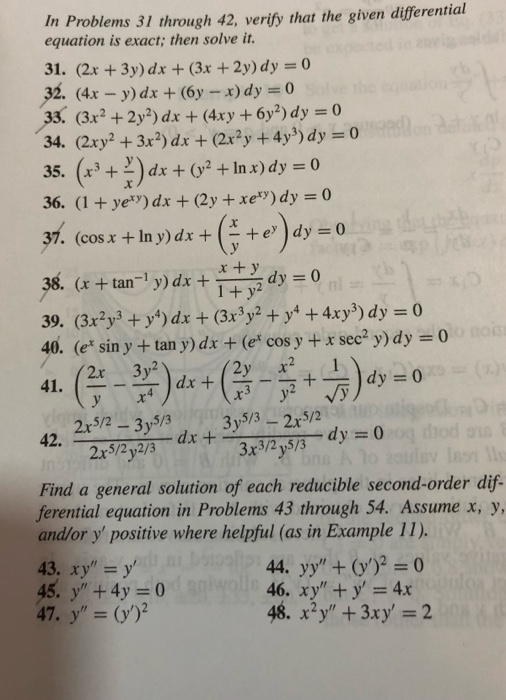
Solved In Problems 31 Through 42 Verify That The Given Chegg Com

How To Solve The Differential Equation 2x 3y Dx 4x Y Dy 0 Quora

The Solution Of Y 2x 2y E X Dx E X Y 3 Dy 0 If Y 0 1 Is Sarthaks Econnect Largest Online Education Community

Engineering Mathematics Notes

What Is The General Solution Of Y 4x Y Dx 2 Y X 2 Dy 0 Quora

What Is The Solution To The Differential Equation Dy Dx 2x Y 1 4x 2y 1 Quora

Pdf 2 6 Exact Differential Equations And Integrating Factors Mirna Mansour Academia Edu

How To Solve 6x 2 Y 4x Dx 2x 3 6y Dy 0 Quora

1

Solved The General Or Particular Solution As Corresponds 1 Sx 4y Dx 4x 8y3 Dy 0 2 Ex Y Dx 2 X Yey Dy 0 Y 0 1

What Are The General Solutions To X X 4 2x 2y 2 Y 4 Dx Ydy 0 Quora

Solved Evaluate The Following Differential Equations Integrating Factor Course Hero

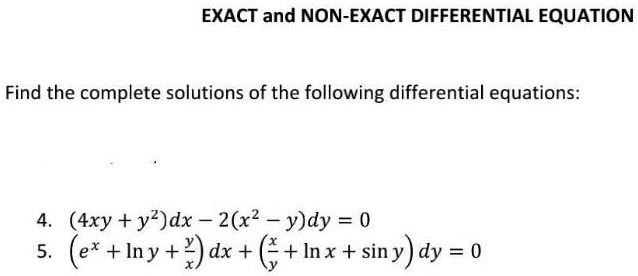
Solved Exact And Non Exact Differential Equation Find The Complete Solutions Of The Following Differential Equations 4xy Y2 Dx 2 X2 Y Dy 0 Ex Iny Y Dx Inx Siny Dy 0

Solved Solve The Following Differential Equation By Variable Separable Course Hero

How To Solve The Following Problem And What Type Of Equation Is It Quora

Solution Of X 2 4xy 2y 2 Dx Y 2 4xy 2x 2 Dy 0 Is

Ordinary Differential Equations 3y 2 X b Dx 2y Y 2 3 b Dy 0 Admits An Integrating Factor Which Is A Function Of X Y 2 Mathematics Stack Exchange

Answered 6 4x 6y 1 Dx 3y 2x 2 Dy Bartleby

Solved 1 Solve The Bvp 6xy 4 Dx 3x 2y Dy 0 Y 2 4 Chegg Com

Solved Solve The General Solution Of The Given Differential Equations Rdx Y2dy B Y Zy X Sin Y Dx Rcosy 2y Dy Y 4x Y Dx 2 X2 Yjdy

Solved Exact Differential Equations 3x 2y Sin Y Dx X X 2 Cos Y Dy Course Hero

Solutions To Homework 2 Introduction To Differential Equations

Solved In Problems 1 22 Solve The Given Differential Equation By Separation Of Variables Dy Sin Sx 2 Dy R 1 2 Dx Dx 3 Dx Er Dy 0 4

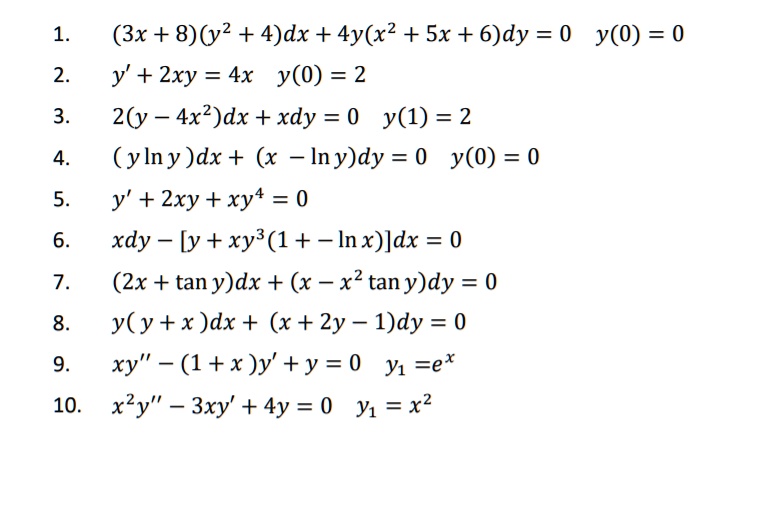
3x 8 Y2 4 Dx 4y X2 Sx 6 Dy 0 Y 0 0 Y Itprospt

Solved Solve Differential Equations By Variable Seperable Dy Dx 4x Xy 2 Y X 2 Y 2 Course Hero

Solve The Differential Equation X 2y Dx 2x Y Dy 0 Youtube

Engineering Mathematics Notes

Solved A Solve The Differential Equation By Exact Chegg Com

Is 1 3 X Sin Y Dx X2 Cos Y Dy 0 Quora

Symbolic Math How To Solve Exact Differential Equations In Matlab Stack Overflow

Solved 1 X Cos 2 Y Dx Tany Dy 0 2 Yin X In Y Dx Dy 0 Chegg Com

Solve X Y 1 Dx 2x 2y 3 Dy 0 Youtube

First Order Ordinary Differential Equations G X Y Y 0

1

Show That The Equation 5x4 3x2y2 2xy3 Dx 2x3y 3xy2 5y4 Dy 0 Is An Exact Differential Equation Find Its Solution Mathematics 2 Question Answer Collection

Incoming Term: y(4x+y)dx-2(x^2-y)dy=0, solution of y(4x+y)dx-2(x^2-y)dy=0,